Buna ziua! Va rog mult sa ma ajutati cu urmatoarele doua probleme si sa le redactati cat mai explicit! Multumesc!
G={ (a,b) ∈ Z x Z ∣ a2 – 2b2 =1 }
Demonstrati ca G este multime infinita.
Fie multimea { fk : IR → IR ∣ fk (x) = (3^k) * x + 2*(3^k) – 2, k∈Z }
Sa se arate ca multimea H = {f3k ∣ k∈Z } este subgrup al grupului (G, °), unde ° este operatia de compunere a functiilor.


1.A demonstra ca multimea G este infinita inseamna a demonstra ca ecuatia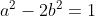 are o infinitate de solutii intregi. Vom face acest lucru demonstrand ca ecuatia are o infinitate de solutii naturale, care sunt desigur si numere intregi. Este de observat ca daca perechea (x, y) este solutie, atunci si perechile (-x, y), (x, -y), respectiv (-x, -y) sunt solutii.
are o infinitate de solutii intregi. Vom face acest lucru demonstrand ca ecuatia are o infinitate de solutii naturale, care sunt desigur si numere intregi. Este de observat ca daca perechea (x, y) este solutie, atunci si perechile (-x, y), (x, -y), respectiv (-x, -y) sunt solutii.
Aceasta ecuatie se numeste ecuatie Pell. Solutia banala a acesteia este (1, 0). Observam ca a este este obligatoriu impar. De aceea, urmatoarea solutie se obtine pt a=3, si b=2. Aceasta solutie este solutia de baza.
Demonstram ca daca (x, y) este o solutie a ecuatiei, cu x si y naturale, atunci si (3x+4y, 2x+3y) este o solutie. Daca (x, y) este solutie, atunci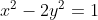 .
.^2-2(2x+3y)^2=9x^2+16y^2+24xy-2(4x^2+9y^2+12xy)=9x^2+16y^2+24xy-8x^2-18y^2-24xy=x^2-2y^2=1)
Daca x si y sunt naturale, atunci si 3x+4y, respectiv 2x+3y sunt naturale. De asemenea, 3x+4y si 2x+3y sunt strict mai mari decat x, respectiv y, deci vom avea astfel o infinitate de solutii, obtinand una noua aplicand recursiv regula „3x+4y, 2x+3y”. Am observat mai sus ca (3, 2) este solutie, care poate fi punct de inceput.
Acest argument poate fi dat si folosind siruri. Daca vrei, pot redacta acest lucru.
2.Mai intai observam ca H este submultime a lui G. H este subgrup al grupului G daca elementul neutru al grupului G se afla in multimea H, si daca oricare ar fi 2 elemente ale lui H, sa zicem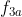 si
si 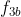 , atunci si
, atunci si 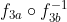 apartine multimii H.
apartine multimii H. 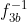 este, desigur, inversul lui
este, desigur, inversul lui 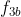 .
.
Sa luam mai intai 2 elemente ale grupului G, adica 2 functii, si sa vedem ce obtinem cand le aplicam operatia grupului, adica operatia de compunere a functiilor. Fie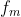 si
si 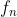 acele elemente:
acele elemente:
(x)=f_m(f_n(x))=f_m(3^n\cdot&space;x+2\cdot3^n-2)=3^m\cdot(3^n\cdot&space;x+2\cdot3^n-2)+2\cdot3^m-2=3^m\cdot3^n\cdot&space;x+2\cdot3^m\cdot3^n-2\cdot3^m+2\cdot3^m-2=3^{m+n}x+2\cdot3^{m+n}-2=f_{m+n}(x))
Mai departe, observam ca grupul G este comutativ:
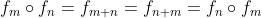 .
.
Folosind aceste lucruri, sa gasim elementul neutru. Elementul neutru este o functie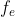 cu proprietatea ca, oricare ar fi o alta functie
cu proprietatea ca, oricare ar fi o alta functie  din grupul G,
din grupul G, 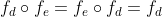 . Dar, stiind ca grupul este comutativ, este suficient sa aratam ca
. Dar, stiind ca grupul este comutativ, este suficient sa aratam ca 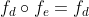 :
:
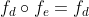

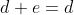
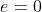
Deci functia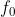 este elementul neutru al grupului G. Daca calculam formula lui f, vom observa ca aceasta este chiar functia identitate, care este in general element neutru la compunerea de functii.
este elementul neutru al grupului G. Daca calculam formula lui f, vom observa ca aceasta este chiar functia identitate, care este in general element neutru la compunerea de functii.
Urmatorul pas este sa observam ca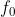 se afla in multimea H, deoarece 0 este un multiplu de 3.
se afla in multimea H, deoarece 0 este un multiplu de 3.
Mai departe, sa cercetam inversele elementelor din G. Inversul elementului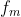 este un element
este un element 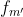 cu proprietatea ca
cu proprietatea ca 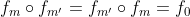 . Deoarece am demonstrat ca G este un grup abelian/comutativ, este suficient sa aratam ca
. Deoarece am demonstrat ca G este un grup abelian/comutativ, este suficient sa aratam ca 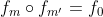 :
:
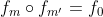

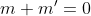
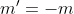
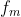 este elementul
este elementul  , altfel spus
, altfel spus 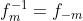 .
.
Deci inversul elementului
Ramane sa demonstram ca oricare ar fi 2 elemente ale lui H, sa zicem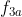 si
si 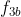 , elementul
, elementul 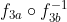 se afla si el in multimea H:
se afla si el in multimea H:
})
}) apartine lui H.
apartine lui H.
Daca a si b apartin lui Z, atunci si a-b apartin lui Z, deci si
Ceea ce am demonstrat mai sus, impreuna cu faptul ca elementul neutru se afla in H este suficient pentru a demonstra ca H este subgrup al lui G.