Subiectele la matematica la evaluarea nationala 2020.
Rezolvarile sunt mai jos, in sectiunea de comentarii.
Update: varianta pdf poate fi descarcata de aici.


Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Subiectul I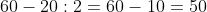
1.
2.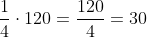
3.10
4.
5.Dreapta DD’ este paralela cu dreapta CC’, deci unghiul dintre DD’ si BC este egal cu unghiul dintre CC’ si BC, adica unghiul BCC’, care este de 90 de grade.
6.Din diagrama, procentul de gutui este de 20%. Cantitatea totala este de 100 de kg. 20% din 100 este 20, deci avem 20 de kg de gutui.
Subiectul II
1.Se deseneaza un cub obisnuit si se noteaza varfurile cu A, B…G, H.
2.Calculam mai intai numerele a si b:
:\frac1{12}=(\frac34-\frac24)\cdot12=\frac14\cdot12=\frac{12}4=3)
=3\cdot(\frac46-\frac36+\frac16)=3\cdot\frac26=\frac66=1)
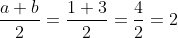
Media aritmetica a lui a si b este
3.Notam cu a suma economisita de Ana si m pe cea economisita de Mihai. Atunci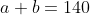 si
si 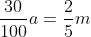 . Din a 2-a relatie, obtinem ca:
. Din a 2-a relatie, obtinem ca:
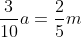
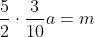
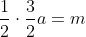
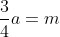
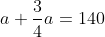
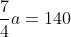
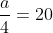
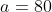
Inlocuim in prima relatie:
Suma economisita de Ana este deci de 80 de lei.
4.a)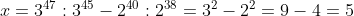
\cdot\sqrt5+(\sqrt3-\frac1{\sqrt3}):\frac1{3\sqrt3}=1+5+(\sqrt3-\frac1{\sqrt3})\cdot3\sqrt3=6+3\cdot3-3=6+9-3=12)
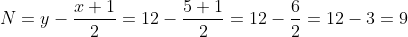
b)Calculam numarul y:
Cel mai mic numar natural de 2 cifre divizibil cu 9 este 18(2*9).
5.=(2x+1)^2-3(x-1)^2-(x-1)(x+1)-6(x+1)=(4x^2+4x+1)-3(x^2-2x+1)-(x^2-1)-6x-6=4x^2+4x+1-3x^2+6x-3-x^2+1-6x-6=4x+1-3+1-6=4x-7)
\leq-1)
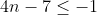
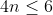
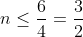
Cum n este natural, solutiile sunt 0 si 1.
Subiectul III=2(13+10)=2\cdot23=46)
}{2}=\frac{10\cdot10\cdot\sin(60)}2=50\cdot\frac{\sqrt3}2=25\sqrt3)
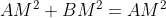
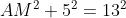
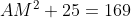
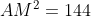
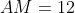
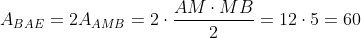
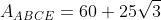 .
.
1.a)
b)Deoarece BC si EC sunt congruente si BC si AD sunt congruente, rezulta ca AD si EC sunt congruente. Deoarece DE e paralel cu AC, rezulta ca ADEC este un trapez isoscel. AE si CD sunt diagonalele trapezului, deci, acesta fiind isoscel, sunt congruente. Deoarece AB si CD sunt congruente, rezulta ca AB si AE sunt congruente.
c)Triunghiul BCE este isoscel cu un unghi de 60 de grade, deci echilateral. Aria sa este:
Deoarece AM este mediatoare in triunghiul BAE, rezulta ca unghiul AEB este drept. Deoarece AM este mediatoare, M este mijlocul lui BE(care este egal cu BC=10 din faptul ca BCE este echilateral), deci BE=5. Aplicam teorema lui Pitagora in triunghiul AMB:
Deoarece M este mijlocul lui BE, AM este mediana in triunghiul BAE. Mediana imparte un triunghi in 2 triunghiuri de arii egale. Cum triunghiul AMB este dreptunghic, rezulta ca:
Aria patrulaterului ABCE este suma ariilor lui BAE si BCE, deci
2.a)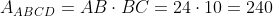
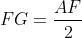 . AF este inaltime in triunghiul dreptunghic ABD, deci
. AF este inaltime in triunghiul dreptunghic ABD, deci 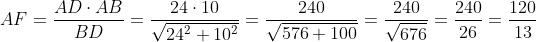 . FG este jumatate din AF, adica exact valoarea ceruta.
. FG este jumatate din AF, adica exact valoarea ceruta.
b)M este mijlocul lui AB, N al lui AD si P al lui AE, deci MN, NP si MP sunt linii mijlocii in triunghiurile ABD, ADE si ABE. Rezulta ca MN||BD, MP||BE si NP||DE. Rezulta ca planele (MNP) si (BDE) sunt paralele.
c)Fie AF perpendiculara din A pe BD. Deoarece EO este perpendiculara pe planul (ABC), care il contine si pe AF, rezulta ca EO perpendiculara pe AF, deci planul (BDE) este perpendicular pe AF. Fie G intersectia lui AF cu MN. Deoarece (BDE) este paralel pe (MNP) si (BDE) perpendicular pe AF, rezulta ca AG perpendicular pe (MNP). Rezulta ca FG este distanta de la planul (MNP) la planul (BDE).
Din faptul ca M este mijlocul lui AB si N al lui AD, MN este linie mijlocie in triunghiul ABD, deci MN||BD. Cum G apartine lui MN, rezulta ca NG||BD. Deoarece N este mijlocul lui AD, rezulta ca NG este linie mijlocie in triunghiul ADF, deci G este mijlocul lui AF, adica
Ma ajuta cineva va rog si pe mine la întrebarea mea 😭😭😭Va rog