Impartind polinomul ![]() la
la ![]() se obtine catul
se obtine catul ![]() si restul
si restul ![]() ,impartind polinomul
,impartind polinomul ![]() la
la ![]() se obtine catul
se obtine catul ![]() si restul
si restul ![]() ,iar continuand procedeul si definind recursiv polinoamele
,iar continuand procedeul si definind recursiv polinoamele ![]() si restul
si restul ![]() ca fiind ,respectiv, catul si restul impartirii lui
ca fiind ,respectiv, catul si restul impartirii lui ![]() la
la ![]() ,pentru orice
,pentru orice ![]() , sa se determine
, sa se determine ![]() .
.
a) 1 b)2 c)7 d) 70 e)100 f) 700
………………………………………………………………………
![]()
Apoi
![]()
Ptr. x=1 avem ![]() , apoi
, apoi ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() si
si ![]()
Analog gasim ![]() si
si ![]()
![]() si
si ![]()
![]() si
si ![]() si raspunsul ar fi d)
si raspunsul ar fi d)
…………………………………….
Daca continuam obtinem :
![]() si
si ![]()
![]() si
si ![]()
![]() si
si ![]()
![]()
…………………………………
Metoda mi se pare cam „muncitoreasca”.Ma gandesc ca trebuie sa existe una mai simpla …mai ales ca observati resturile se repeta.Poate ma ajuta cineva cu o varianta mai usoara de rezolvare,pe care eu inca nu am descoperit-o.
Multumesc.


Da, exista o metoda mai rapida care nu necesita impartirea efectiva.
Avem , apoi
, apoi  .. observam de aici ca, continuand analog, obtinem:
.. observam de aici ca, continuand analog, obtinem:
Vrem sa scapam de polinomul de langa ca sa putem pune
ca sa putem pune  .. ne gandim sa derivam de 4 ori.
.. ne gandim sa derivam de 4 ori.
Sa observam ca polinomul are pe
are pe  radacina de ordinul 5, deci
radacina de ordinul 5, deci  (derivata de ordin 4 se anuleaza in
(derivata de ordin 4 se anuleaza in  ), deci daca derivam de
), deci daca derivam de  ori si punem
ori si punem  scapam si de polinomul
scapam si de polinomul  . Derivand expresia
. Derivand expresia  de 4 ori si observand ca
de 4 ori si observand ca  sunt constante, obtinem
sunt constante, obtinem  . Punand
. Punand  , obtinem
, obtinem  .
.
Poate mai elementar, dacă observăm că, pe de o parte

![Rendered by QuickLaTeX.com X^8=[1+(X-1)]^8=1+C_8^1(X-1)+... +C_8^8(X-1)^8](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-fb287f0db26de2ca2abd34ce8c82cc79_l3.png)
 , deci
, deci 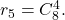
iar pe de altă parte,
deducem
Multumesc mult,domnilor ghioknt si PhamtomR.Doua solutii inedite.
Bună dimineața,
Notând , atunci restul căutat este egal cu restul
, atunci restul căutat este egal cu restul  în cazul în care este vorba despre polinomul
în cazul în care este vorba despre polinomul  și monomul
și monomul  de unde se observă imediat că
de unde se observă imediat că  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Numai bine,
Integrator