Home/ Intrebari/Q 82719
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

Gina - Ioana
Pe: 2013-09-07T17:33:28+03:00 In: In:

Exercitiu la algebra

Determinati numerele reale x si y, stiind ca {x^2} + {y^2} - 6\sqrt 3 x + 4\sqrt 5 y + 47 = 0.

As scadea 47 din 0, dar nu stiu daca e corect.De aici nu mai am nici o idee de rezolvare. M-ati putea ajuta?

Similare

7 raspunsuri

  1. Green eyes
    maestru (V)

    Salut,

    Te rog să verifici enunţul pe care l-ai scris, mă refer la partea:

    \bl -6\cdot\sqrt{3}\cdot x+4\cdot\sqrt{5}\cdot x

    Este x în ambii termeni, sau în primul este x şi la al doilea avem y ? Mulţumesc.

    Green eyes.

  2. bedrix
    expert (VI)

    Dupa ce corectezi enuntul , prelucrezi membrul stang si ar trebui sa ajungi la suma a 2 patrate , unul in functie de x si celalalt in functie de y.

  4. Gina - Ioana

    M-am corectat.

  5. bedrix
    expert (VI)

    Indicatie : scrie 47 ca 27+20 si formeaza patratele
    Foloseste: (a+b)^2 = a^2 + 2ab + b^2 , a si b E R

  6. Gina - Ioana

    Am incercat sa rezolv asa, dar nu cred ca e corect:
    \begin {x^2} - 2 \cdot 3\sqrt 3 x + {(\sqrt {47} )^2} + {y^2} + 2 \cdot 2\sqrt 5 y + {(\sqrt {47} )^2} = 0{\left/{{} {:2}}} \Rightarrow {x^2} - 3\sqrt 3 x + 47 + {y^2} + 2\sqrt 5 y + 47 = 0{\left/ {{} {:47}}}\Rightarrow {x^2} - 3\sqrt 3 x + {y^2} + 2\sqrt 5 y = 0\Rightarrow {x^2} + {y^2} = 3\sqrt 3 x - 2\sqrt 5 y/{{} {:x}}\Rightarrow x + {y^2} = 3\sqrt 3 - 2\sqrt 5 y/ {{} {:y}}\Rightarrow x + y = 3\sqrt 3 - 2\sqrt 5

  8. bedrix
    expert (VI)

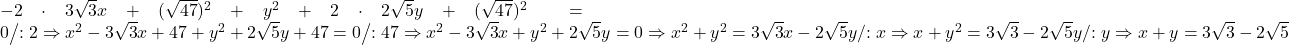
    Nu este corect.
    Incearca sa folosesti indicatia de mai sus , unde 27=(3*SQRT3)^2 si 20=(2*SQRT5)^2

  9. andu

    Gina – Ioana wrote: Determinati numerele reale x si y, stiind ca {x^2} + {y^2} - 6\sqrt 3 x + 4\sqrt 5 y + 47 = 0.

    \it{\bl \Large x^2+y^2-6sqrt3x+4\sqrt5y +47 = 0 \Longleftrightarrow x^2+y^2-6sqrt3x+4\sqrt5y +27 + 20 = 0 \Longleftrightarrow x^2-6\sqrt3x +y^2 +4\sqrt5y + (3\sqrt3)^2 + (2\sqrt5)^2 =0 \Longleftrightarrow \\\;\\ \\\;\\ [ x^2-6\sqrt3x + (3\sqrt3)^2] + [y^2 +4\sqrt5y + (2\sqrt5)^2] = 0 \Longleftrightarrow (x-3\sqrt3)^2 + (y+2\sqrt5)^2 = 0}

Raspunde

Raspunde