Sa se rezolve in multimea numarelor intregi sistemul:
![]()
va rooog frumos!!!
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Sa remarcam ca
si analog pentru y si z.
Apoi sa analizam ce semne pot avea numerele x,y,z.
Daca toate trei sunt pozitive contradicita este evidenta.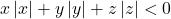 , iarasi contradictie.
, iarasi contradictie.
Daca toate trei sunt negative, atunci
In concluzie doua radacini sunt nenegative iar cea de a treia negativa sau una este nenegativa iar celelalte doua negative.
In prima situatie, fie
. Atunci sistemul devine:
Scazand cele doua ecuatii se obtine usor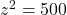 , fara solutie in multimea numerelor intregi.
, fara solutie in multimea numerelor intregi.
In cea de a doua situatie, fie
. Atunci sistemul devine:
Insumand cele doua ecuatii rezulta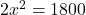 , cu solutia
, cu solutia 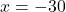 .
.
Mai departe ramane sa rezolvati ecuatia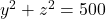 . Se observa rapid solutia solutia (-20, -10) dar puteti verifica efectiv, prin incercari, daca mai exista si o alta solutie.
. Se observa rapid solutia solutia (-20, -10) dar puteti verifica efectiv, prin incercari, daca mai exista si o alta solutie.
nu, numai -20, -10 si -10, -20
multzam