Punctul b, va rog!
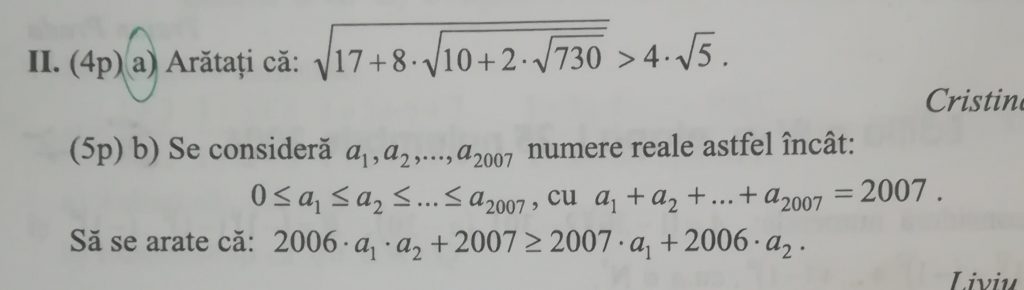
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Trecem totul in partea stanga:
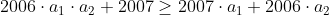
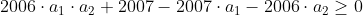
+2007(1-a_1)\geq0)
(2006a_2-2007)\geq0)
Daca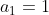 , inegalitatea este clar adevarata.
, inegalitatea este clar adevarata.
Daca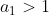 , atunci, deoarece
, atunci, deoarece 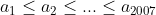 , rezulta ca
, rezulta ca  si atunci suma lor va fi mai mare decat 2007. Rezulta ca
si atunci suma lor va fi mai mare decat 2007. Rezulta ca 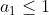 . Am spus deja ca inegalitatea este adevarata pt
. Am spus deja ca inegalitatea este adevarata pt 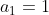 . Ne ocupam mai departe de cazul
. Ne ocupam mai departe de cazul 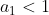 .
.
Daca
De ce este necesar ca 2006 a2 – 2007 <sau = cu 0. De unde ai luat?
Dupa ce am spus ca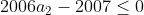 ,am demonstrat ca nu este posibil sa fie mai mare decat 0, pentru ca am obtine o suma mai mare decat 2007.
,am demonstrat ca nu este posibil sa fie mai mare decat 0, pentru ca am obtine o suma mai mare decat 2007.
Da dar de ce 2006 a2?
Inegalitatea de demonstrat este(2006a_2-2007)\geq0)
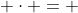 ,
,  ). Cum
). Cum 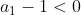 (am analizat separat cazul cand este 0), rezulta ca
(am analizat separat cazul cand este 0), rezulta ca 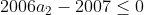 .
.
Ambele paranteze trebuie sa aiba acelasi semn(
Da, acum am înțeles