Va rog sa o rezolvati!
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Sa zicem ca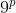
si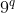 
sunt cele 2 elemente alese. Daca 
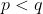, atunci cele 2 elemente sunt inlocuite cu 
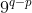. Daca 
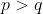, atunci elementele sunt inlocuite cu 
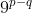. Altfel spus, elementele sunt inlocuite cu 
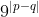. Observam ca aceasta operatie este echivalenta cu alegerea a 2-a numere din sirul 
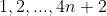si inlocuirea acestora cu modulul diferentei lor.
Observam ca sirul are un numar impar de termeni impari((4n+2)/2=2n+1).
Daca cele 2 elemente alese sunt impare, numarul ce le inlocuieste este par, iar numarul de termeni impari scade cu 2, deci ramane tot impar.
Daca cele 2 elemente alese sunt pare, numarul ce le inlocuieste este par, deci numarul de termeni impari ramane impar.
Daca unul dintre termeni este par si celalalt este impar, atunci numarul de termeni impari ramane acelasi, deoarece eliminam un termen impar si il inlocuim cu un alt termen impar.
Deci la fiecare pas numarul de termeni impari din sir este impar. Rezulta ca atunci cand mai ramane un singur termen in sir, acesta trebuie sa fie impar(altfel numarul de termeni impari ar fi 0, care nu este impar).
Ne intoarcem la sirul original. Am stabilit ca ultimul exponent este impar, deci ultimul termen ramas este de forma^k\cdot9=(81)^k\cdot9)
. Ultima cifra a lui 
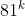este aceeasi cu ultima cifra a lui 
, adica 1. Rezulta ca ultima cifra a lui 
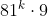este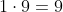 
Mulțumesc! Ai rezolva o astfel de problema chiar si pentru un punct??? Ca sa stiu cum imi gestionez punctele.
Cu placere! De obicei nu ma uit la cate puncte are o problema. Oricum am cele mai multe puncte de pe site.