Home/ Intrebari/Q 86201
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

ella22
Pe: 2014-04-07T19:42:16+03:00 In: In:

problema admitere

Se considere sirul (a_n), cu n apartine N\{0}, definit astfel:
a_1=2,a_2=1 si

\frac{2}{a_n}=\frac{1}{a_{n-1}}+\frac{1}{a_{n+1}} pentru n>1.

Atunci \lim_{n\to\infty}{a_n}:
A.1
B.2
C.+\infty
D.nu exista
E.0

Similare

5 raspunsuri

  1. DD
    profesor

    Relatia de recurenta se poate scrie si;
    1/an-1/a(n-1)=1/a(n+1)-1/an
    1/a(n-1)-1/a(n-2)=1/an-1/a(n-1)
    …………………………………………
    1/a3-1/a2=1/a4-1/a3
    1/a2-/a1=1/a3-1/a2 adunam aceste relatii
    –––––––––
    1/a2-1/a1=1/a(n+1)-1/an=1-1/2=1/2
    Sa iteram si aceasta ultima relatie
    1/a(n+1)-1/an=1/2
    1/an-1/a(n-1)=1/2
    ………………………
    1/a2-1/a1=1/2 adunamsi avem;1/a(n+1)=(1/2)^n, sau a(n+1)=2^n
    lim(n->infinit)an=2^(n-1)->infinit. raspuns C)

  2. DD
    profesor

    ERATA
    In ultimile doua randuri, ca rezultat al adunarii, NU este ce am scris . Rezultatul este ;
    1/a(n+1)-1/a1=n/2 sau ; 1/a(n+1)=(n+1)/2 sau ; a(n+1)=2/(n+1), respectiv
    an=2/n si lim(n->infinit)[2/n]->0 Raspuns E)
    SCUZE!

  4. ella22

    In cazul sirului x_n,n>=0 definit prin 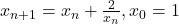x_{n+1}=x_n+\frac{2}{x_n},x_0=1, am incercat sa merg pe acelasi principiu, trecand pe x_n in partea stanga, dar nu am reusit sa obtin vreun rezultat. Ce artificiu as mai putea sa-i fac?
    Multumesc pentru rezolvarea anterioara!

  5. PhantomR
    expert (VI)

    Trebuie sa-i aflati limita? Atunci putem face astfel:

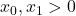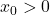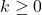    Sa observam ca x_2=1+2=3, deci x_0,x_1>0. Pe baza relatiei de recurenta, intuim ca x_n>0,n\geq 0 si demonstram prin inductie. Pentru etapa verificarii, avem x_0>0. Presupunem x_k>0 pentru k\geq 0 fixat. Din relatia de recurenta obtinem 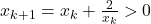x_{k+1}=x_k+\frac{2}{x_k}>0, deci conform Principiului inductiei matematice, x_n>0,\forall n\geq 0.

    Acum, sa observam ca x_{n+1}-x_n=\frac{2}{x_n}>0, adica sirul este (strict) crescator si deci are limita (finita sau infinita). Fie l=\lim_{n\to\infty}x_n. Sa presupunem ca sirul este marginit, deci ca l este finita. Cum sirul este crescator, avem x_n\leq l, iar cum x_n>0 deducem l>0. Trecand la limita cand n\to\infty in relatia de recurenta deducem l=l+\frac{2}{l} \Rightarrow \frac{2}{l}=0, fals. Deci sirul este nemarginit si fiind crescator, inseamna ca limita lui este \fbox{\lim_{n\to\infty} x_n=+\infty}.

  6. ella22

    La sirul x_n nu i se poate gasi cumva termenul general, deoarece mai apare o cerinta la exercitiul acesta, unde se cere sa se calculeze 

    *** QuickLaTeX cannot compile formula:
\lim_{n\to\infty}\frac{x_n}{sqrt{n{}

*** Error message:
File ended while scanning use of \frac .
Emergency stop.

    ?

Raspunde

Raspunde