Se considera triunghiul ABC, punctele A’, B’, C’ mijloacele [BC], [AC], [AB] si M, N, P, Q puncte din plan cu proprietatea ca 4AM=3AB, 5AN=3AC, 5BP=2BC, BQ=2BA. (vectori).
Sa se arate ca dreptele MN si PQ contin centrul de greutate al triunghiului ABC.
dennis9091guru (IV)


Fie G centrul de greutate.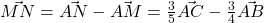
Avem
Rezulta ca vectorii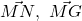 sunt coliniari, deci punctele M, N, G sunt coliniare.
sunt coliniari, deci punctele M, N, G sunt coliniare.
Analog se arata ca punctele P, Q, G sunt coliniare.