Sa se determine unghiurile triunghiului ABC stiind ca 8cosAcosBcosC=1.
Multumesc anticipat.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Salut,
Vezi mai jos.
Green eyes.
care sunt cele doua poze ?
Buna ziua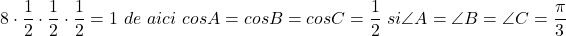
Evident
Triunghiul ABC este echilateral.
Nu se poate spune direct acest lucru doar din acea relatie. Avem si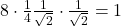 , dar de aici nu rezulta
, dar de aici nu rezulta 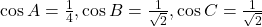 .
.
Buna seara
![Rendered by QuickLaTeX.com Definim \ o\ functie\ f(cosA,cosB,cosC)=cosA\cdot cosB\cdot cosC\ \\cu\angle A,B,C\in \ \triangle ABC. Aceasta \ functie \ pe \ intervalul\ [0,\pi] este\ o\ functie\ strict\ monotona\\ \ si\ la \ fel \ si \ functiile\ cos.](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-9bb67209754fee1be0327999fb4fb33c_l3.png)
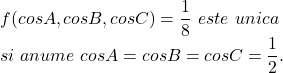
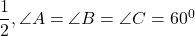 iar triunghiul ABC
iar triunghiul ABC
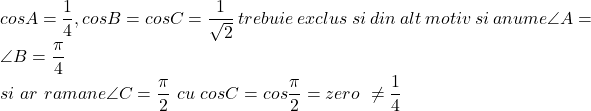
Eu vad in completare rezolvarea problemei in felul urmator:
Din acest motiv solutia pentru
Demonstrarea se mai poate face prin reducere la absurd si anume:presupun ca ar mai exista si o alta solutie
pentru cosA,cosB,cosC in afara celei aratate mai sus.
Dar aceasta contrazice ipoteza unicitatii solutiei in cazul unor functii strict monotone.
Deci in concluzie singura solutie pentru problema in cauza este cosA=cosB=cosC=
este echilateral.
Exemplul
Buna ziua,
Functia pe care ati definit-o este o functie de trei variabile, deci am putea zice ca e definita pe![Rendered by QuickLaTeX.com [0,\pi]\times [0,\pi] \times [0,\pi]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-ac4696ac1df640d4f972d4648574ea97_l3.png) . Se poate defini monotonia si pentru astfel de functii, insa trebuie mai intai o relatie de ordine pe multimea
. Se poate defini monotonia si pentru astfel de functii, insa trebuie mai intai o relatie de ordine pe multimea ![Rendered by QuickLaTeX.com [0,\pi]^3](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-1bc943cdf2390ac9786c6397e04e84ee_l3.png) , insa este alta treaba decat in cazul functiilor definite pe
, insa este alta treaba decat in cazul functiilor definite pe  .
.
Contraexemplul pe care l-am dat arata ca exista alte solutii pentru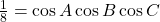 daca folosim, de exemplu, doar restrictia
daca folosim, de exemplu, doar restrictia ![Rendered by QuickLaTeX.com A,B,C\in [0;\pi]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-606840146f379b3dcd6e5216432f8565_l3.png) , iar in postarea dumneavoastra pare ca nu ati folosit faptul ca
, iar in postarea dumneavoastra pare ca nu ati folosit faptul ca  este triunghi decat pentru a determina unghiurile la final, aparent tragand concluzia ca
este triunghi decat pentru a determina unghiurile la final, aparent tragand concluzia ca 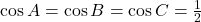 doar din relatia mentionata la inceputul postarii:
doar din relatia mentionata la inceputul postarii: 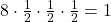 .
.
Buna ziua
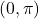 poate conduce la a arata ca si functia cosAcosBcosC este strict monotona pe acest interval situatie
poate conduce la a arata ca si functia cosAcosBcosC este strict monotona pe acest interval situatie
Asa este.
Faptul ca cos este o functie strict monotona pe intervalul
in care solutia gasita este unica.
Unica ? Nu este unica. Noi avem in esenta relatia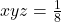 pentru
pentru ![Rendered by QuickLaTeX.com x,y,z\in [-1,1]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-544f40d132b2c8c1e5420c47dbdbea3a_l3.png) , iar aceasta are o infinitate de solutii:
, iar aceasta are o infinitate de solutii: ![Rendered by QuickLaTeX.com (x,y,z)\in [-1,1]^3](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-3deaa47715244605360e9bce8eaf7721_l3.png) . De exemplu,
. De exemplu, 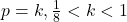 si
si 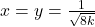 .
.
Cred ca a fost neglijata conditia ca A,B,C reprezinta unghiurile unui triunghi si deci
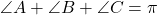
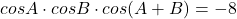
In acest caz avem ca
Deci relatia este supusa la numai doua grade de libertate.
Problema este de a demonstra ca aceasta functie este strict monotona.
Nu pot crede ca problema are o infinitate de solutii.
Va rog sa ma iertati daca am fost cumva prea dur in ce am scris:(. Problema in sine are o singura solutie😀 , ceea ce am vrut eu sa subliniez este ca nu se poate deduce din egalitatea 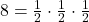 ca neaparat
ca neaparat 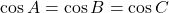 doar pentru ca
doar pentru ca  sunt din
sunt din ![Rendered by QuickLaTeX.com [0;\pi]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-1c7d3a46892c8d0cdf51eadf94f309ca_l3.png) (pentru ca asa pare in postul pe care l-ati scris initial
(pentru ca asa pare in postul pe care l-ati scris initial 😀 ). Daca se adauga si conditia 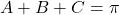 (
( triunghi cu aceasta egalitate si cu intervalul impus asupra
triunghi cu aceasta egalitate si cu intervalul impus asupra  (e de fapt destul ca
(e de fapt destul ca 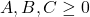 , marginea superioara rezultand din egalitatea anterioara), atunci problema are intr-adevar o singura solutie.
, marginea superioara rezultand din egalitatea anterioara), atunci problema are intr-adevar o singura solutie.
Am inteles asa este!
O metoda:
O idee:
Din teorema cosinusului rezultă valorile
Triunghiul nu poate fi si ascutit si echilateral in acelasi timp?
Orice triunghi echilateral este evident ascutitunghic, deoarece masura fiecarui unghi este de 60 grade.
Deci raspunsul la intrebarea ta este: se poate…ba chiar mai mult, acest lucru se-ntampla mereu.