Home/ Intrebari/Q 85639
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

xor_NTG
maestru (V)
Pe: 2014-02-25T17:45:00+02:00 In: In:

Problema ecuatie cu parametru

Multimea valorilor lui m real pentru care

    \[ 2\ln \left| x \right| = mx^2 + 1 \]

este:

    \[ \begin{array}{l} a)\,\,\,\,m \in \left( { - \infty , - \frac{1}{{e^2 }}} \right] \cup \left[ {\frac{1}{{e^2 }},1} \right] \\ b)\,\,\,m \in \left[ {\frac{1}{{e^2 }},\infty } \right) \\ c)\,\,\,m \in \left\{ {\frac{1}{{e^2 }}} \right\} \cup \left( {1,e} \right] \\ d)\,\,m \in \left( { - \infty ,0} \right] \cup \left\{ {\frac{1}{{e^2 }}} \right\} \\ e)\,\,m \in \left( { - \infty , - \frac{1}{{e^2 }}} \right] \\ f)\,m \in \left( { - \infty ,1} \right) \\ \end{array} \]

Eu am incercat să aduc această ecuatie la o formă abordabilă…

    \[ 2\ln \left| x \right| = mx^2 + 1 \Leftrightarrow \ln \left| x \right|^2 = mx^2 + 1 \Leftrightarrow \ln x^2 = mx^2 + 1 \Leftrightarrow x^2 = e^{mx^2 + 1} \]

Acum, conditia pentru ca ecuatia să aibă două solutii, este ca discriminantul ecuatiei de gradul 2 de la exponentul membrului drept, să fie mai mare sau egal cu zero, ceea ce implică m \in (-\infty, 0]

Acum observăm că singura variantă care implică acest interval este varianta d), doar că mai apare acolo acel

    \[ \frac{1}{{e^2 }} \]

pe care nu am idee de unde il pot lua.

Am trasat graficul celor două functii din ultima formă a egalitătii (cu geogebra) si am studiat dependenta de m a intersectiei celor două curbe în două puncte distincte.

Aveti aici o imagine a graficului: http://s2.postimg.org/sx90kopgp/logaritm.jpg

Graficul este „surprins” în momentul în care m este foarte aproape de

    \[ \frac{1}{{e^2 }} \]

. Dacă scad m-ul, parabola din interior se „desface” din ce în ce mai mult. Când pun m=0, este o linie orizontală, iar dacă m-ul este negativ, parabola respectivă devine concavă, dar „capetele” ei sunt alungite spre sensul negativ, respectiv spre sensul pozitiv al axei OX, deci oricum intersectează cealaltă parabolă.

În urma analizei graficului, am observat că cele două curbe se întâlnesc în exact două puncte pentru orice m în intervalul

    \[ \left( { - \infty ,\frac{1}{{e^2 }}} \right) \]

Care e explicatia? E cumva o gresală în exercitiu? Sau am interpretat eu ceva gresit?

Multumesc.

Similare

2 raspunsuri

  1. ghioknt
    profesor

    Ai scris:
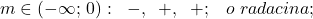
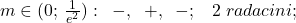
    Acum, conditia pentru ca ecuatia să aibă două solutii, este ca discriminantul ecuatiei de gradul 2 de la exponentul membrului drept, să fie mai mare sau egal cu zero, ceea ce implică…
    Exponentul respectiv este o funcţie de gradul 2, nu o ecuaţie. Un exponent poate lua orice valoare reală, chestia cu discriminantul …
    Răspunsul corect mi se pare a fi (-\infty;\,\frac{1}{e^2}].
    Să observăm că în ecuaţie intră numai funcţii pare, deci dacă a este o soluţie, atunci şi -a este soluţie. Deci este suficient
    să studiem ecuţia doar pe intervalul (0; oo). Eu aş pune-o sub forma \frac{2\ln x-1}{x^2}-m=0 şi aş studia
    şirul lui Rolle asociat funcţiei f(x)=\frac{2\ln x-1}{x^2}-m şi intervalului (0; oo).
    f'(x)=0\Leftrightarrow \frac{4-4\ln x}{x^3}\Leftrightarrow x=e.
    Şirul lui Rolle este format din semnele expresiilor R_1=f(0+0)=-\infty;\;R_2=f(e)=\frac{1}{e^2}-m;\;R_3=\lim_{x\to\infty}f(x)=-m.
    m\in (-\infty;\,0):\;\;-,\;\;+,\;\;+;\;\;\;o\; radacina;
    m=0:\;\;\;-,\;\;+,\;\;0;\;\;\;o\;radacina;
    m\in(0;\,\frac{1}{e^2}):\;\;-,\;\;+,\;\;-;\;\;\;2\;radacini;
    m=\frac{1}{e^2}:\;\;\;-,\;\;0,\;\;-;\;\;\;o\;radacina\;x=e;
    m\in(\frac{1}{e^2};\,\infty):\;\;-,\;\;-,\;\;-;\;\;\;nicio\;radacina.
    Cu bine,
    ghioknt

  2. xor_NTG
    maestru (V)

    Deci n-are nici o treabă acea conditie pe care am pus-o eu (cu delta pozitiv).

    Foarte ingenioasă abordarea cu sirul lui Rolle.

    În conlcuzie, nicio variantă nu este corectă?

    Multumesc cu respect.

Raspunde

Raspunde