Home/ Intrebari/Q 79508
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

dennis9091
guru (IV)
Pe: 2012-12-13T12:51:49+02:00 In: In:

inegalitate

Fie a,b,c>sau egal cu 0. astfel incat a^2+b^2+c^2=3. Sa se arate ca:
(a^3+a+1)(b^3+b+1)(c^3+c+1)<sau egal cu 27.

Similare

22 raspunsuri

  1. ali
    maestru (V)

    Daca nu v-a fi trimis subiectul în zona carantina atunci voi posta o solutie (folosind inegalitatea lui Cebasev)….. Nu vreau ca munca mea sa ajungă la „gunoi”….

    [hr]Propun ca în momentul în care un subiect este mutat sau trimis la gunoi de moderator/admin sa se precizează si motivul !

  2. DD
    profesor

    Attached files

  4. dennis9091
    guru (IV)

    DD wrote:


    Cum pot sa descarc imaginea pe care ai pus’o ? Multumesc!

  5. dennis9091
    guru (IV)

    ali wrote: Daca nu v-a fi trimis subiectul în zona carantina atunci voi posta o solutie (folosind inegalitatea lui Cebasev)….. Nu vreau ca munca mea sa ajungă la „gunoi”….

    [hr]Propun ca în momentul în care un subiect este mutat sau trimis la gunoi de moderator/admin sa se precizează si motivul !


    Iti multumesc daca ma vei putea ajuta postand o solutie..

  6. dennis9091
    guru (IV)

    Multumesc mult DD.

  8. ali
    maestru (V)

    DD wrote:


    Foarte buna solutie …. bravo !

    Iti multumesc daca ma vei putea ajuta postand o solutie..


    Nu cred ca mai ai nevoie …. Solutia lui DD este foarte scurta si foarte simpla…. mai mult de cât atât nu se poate….

    Ps: dacă vrea cineva neapărat sa vadă si o solutie folosind inegalitatea lui cebasev … atunci voi posta si eu varianta mea (este mai lunga) !

  9. dennis9091
    guru (IV)

    Iti multumesc . Varianta lui DD este exceptionala.

  10. MathDa

    DD wrote:

    Nu te supara dar pt ca Mg<=Ma si daca Ma>=3 nu rezulta neaparat ca Mg<=3 deci tu ar trb sa demonstrezi ca Ma<=3

  12. MathDa

    se poate demonstra a^3+a+1<=3a^2 <=>a^3+a-2a^2+1-a^2<=0<=>
    (rad(a^3)+rad(a))^2-a^2<=-1<=>a(a-1-rad(a))(a-1+rad(a))<=-1;
    observam ca a-rad(a) este mai mare cu cat a ul este mai mare si a este maxim rad(3) efectuand calculele pt a=rad(3) se obtine un adevar,in mod analog se dem b^3+b+1<=3b^2 si c^3+c+1<=3c^2.Immultind relatiile obtine (a^3+a+1)(b^3+b+1)(c^3+c+1)<=3^3(abc)^2 si cum a^2+b^2+c^2=3=> cu Ma>=Mg ca (abc)^2<=1 de unde => concluzia

  13. dennis9091
    guru (IV)

    MathDa wrote: [quote=DD]

    Nu te supara dar pt ca Mg<=Ma si daca Ma>=3 nu rezulta neaparat ca Mg<=3 deci tu ar trb sa demonstrezi ca Ma<=3
    Ai dreptate.

  14. ali
    maestru (V)

    pt ca Mg<=Ma si daca Ma>=3 nu rezulta neaparat ca Mg<=3


    Citind ce ai scris … da! … cred ca ai dreptate ….

    (rad(a^3)+rad(a))^2-a^2<=-1<=>a(a-1-rad(a))(a-1+rad(a))<=-1;


    Aici cred ca-ti scapă ceva (nu-s 100% sigur, ar fi preferabil sa folosesti codul latex)…

    observam ca a-rad(a) este mai mare cu cat a ul este mai mare si a este maxim rad(3)


    Daca esti într-o sala de examen … atunci nu este suficient ce afirmi …. Ca sa afirmi ceva trebuie sa si-l demonstrez …. deci apare un „minus” în solutia ta !
    Pe cuvântul meu, devin extrem de fericit când vad si alte solutii … alte idei fata de ale mele (care de obicei sunt complicate)…. însă ideea ta… sigur este incompleta !
    De exemplu…. încă nu mai convins cu a^3+a+1<=3a^2 ?!

  16. dennis9091
    guru (IV)

    ali wrote:

    pt ca Mg<=Ma si daca Ma>=3 nu rezulta neaparat ca Mg<=3


    Citind ce ai scris … da! … cred ca ai dreptate ….

    (rad(a^3)+rad(a))^2-a^2<=-1<=>a(a-1-rad(a))(a-1+rad(a))<=-1;


    Aici cred ca-ti scapă ceva (nu-s 100% sigur, ar fi preferabil sa folosesti codul latex)…

    observam ca a-rad(a) este mai mare cu cat a ul este mai mare si a este maxim rad(3)


    Daca esti într-o sala de examen … atunci nu este suficient ce afirmi …. Ca sa afirmi ceva trebuie sa si-l demonstrez …. deci apare un „minus” în solutia ta !
    Pe cuvântul meu, devin extrem de fericit când vad si alte solutii … alte idei fata de ale mele (care de obicei sunt complicate)…. însă ideea ta… sigur este incompleta !
    De exemplu…. încă nu mai convins cu a^3+a+1<=3a^2 ?!


    Ali are dreptate.!

  17. MathDa

    observam ca a-rad(a) este mai mare cu cat a ul este mai mare si a este maxim rad(3)


    Daca esti într-o sala de examen … atunci nu este suficient ce afirmi …. Ca sa afirmi ceva trebuie sa si-l demonstrez …. deci apare un „minus” în solutia ta !
    Pe cuvântul meu, devin extrem de fericit când vad si alte solutii … alte idei fata de ale mele (care de obicei sunt complicate)…. însă ideea ta… sigur este incompleta !
    De exemplu…. încă nu mai convins cu a^3+a+1<=3a^2 ?!
    Poi a^2<=3 din ipoteza =>extragand radicalul a<=rad(3)
    cu factor comun rad(a)(rad(a)-1) si atunci aceasta expresie creste in functie de a, cu cat a-ul este mai mare cu atat expresia devine mai mare.
    Multumesc de sfat si te rog sa-mi spui daca am gresit ceva in acest rationament ca sa evit astfel de greseli pe viitor

  18. ali
    maestru (V)

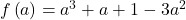    Functia f\left( a \right) = {a^3} + a + 1 - 3{a^2} este descrescătoare pe anumite intervale uite-te la schită:

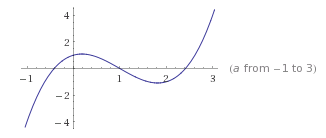
    Adica pentru anumite valori a lui a>0 inegalitatea este falsa, exemplu:
    \begin{array}{l} a = \frac{1}{2}\\ {\left( {\frac{1}{2}} \right)^3} + \left( {\frac{1}{2}} \right) + 1 - 3{\left( {\frac{1}{2}} \right)^2} \le 0 \to {\rm{fals}}\\ {\left( {\frac{1}{2}} \right)^3} + \left( {\frac{1}{2}} \right) + 1 - 3{\left( {\frac{1}{2}} \right)^2} \ge 0 \to {\rm{adevarat}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^3} + \left( {\frac{1}{2}} \right) + 1 \ge 3{\left( {\frac{1}{2}} \right)^2} \end{array}
    Sunt multe de spus legate despre aceste greseli pe care le facem ….. însă cu timpul învătăm sa le ocolim !
    Îti voi da un sfat care mi la dat si mie cândva un coleg de al meu ….
    Când avem o inegalitate de demonstrat … ultima solutie la care ar trebui sa te gândesti este: sa prelucrezi inegalitate pe parti…. mai apoi le aduni/scazi/multiplici/imparti … etc …. astfel riscam sa nu controlam semnul !

  20. MathDa

    Ms mult,mai bn ca am comis aceasta greseala acuma decat sa o fi comis la un concurs sau olimpiada,totusi as vrea sa inteleg cum se rezolva aceasta problema

  21. dennis9091
    guru (IV)

    Si eu as vrea sa vad o rezolvare finala si cat se poate de corecta .

  22. DD
    profesor

    Attached files

  24. ali
    maestru (V)

    Nu ….. aici iti scapă ceva …!
    Dintr-o propozitie falsa se poate obtine un adevăr!
    Deci, dacă inegalitatea initială a fost falsa se putea la fel de frumos sa formulezi din ea o inegalitate care este adevărată!
    In concluzie, o inegalitate matematica nu se poate demonstra plecând de la presupunerea ca inegalitatea initială este adevărata!

  25. ali
    maestru (V)

    Am asteptat sa-mi spune denis de unde a făcut rost de aceasta problema …. dacă era o problema propuse la vreun concurs în desfăsurarea atunci nu puteam posta o solutie (ar fi interzis conform regulamentului)!

    totusi as vrea sa inteleg cum se rezolva aceasta problema


    Solutia completa:
    \begin{array}{l} {a^2} + {b^2} + {c^2} = 3 \Leftrightarrow \left( {{1^2} + {1^2} + {1^2}} \right)\left( {{a^2} + {b^2} + {c^2}} \right) = 9\\ {\rm{CBS}}:\left( {{1^2} + {1^2} + {1^2}} \right)\left( {{a^2} + {b^2} + {c^2}} \right) \ge {\left( {a + b + c} \right)^2} \Leftrightarrow 9 \ge {\left( {a + b + c} \right)^2}\left| {\left( { \uparrow \frac{3}{2}} \right)} \right. \Rightarrow \\ 27 \ge {\left( {a + b + c} \right)^3} \to \left( {{\rm{relatia 1}}} \right)\\ {\left( {{\rm{MA}} - {\rm{MG}}} \right)_3}:{\left( {a + b + c} \right)^3} \ge 27abc \to \left( {{\rm{relatia 2}}} \right)\\ {\rm{relatia 1}}{\rm{,relatia 2}} \Rightarrow \max \left\{ {abc} \right\} = 1.\\ {\rm{Pasul 2) rescriem inegalitatea initiala ca fiind:}}\\ \left( {\frac{{{a^3} + a + 1}}{3}} \right)\left( {\frac{{{b^3} + b + 1}}{3}} \right)\left( {\frac{{{c^3} + c + 1}}{3}} \right) \le 1\\ {\rm{Mai departe}}{\rm{, aplicam inegalitatea lui cebasev:}}\\ \left( {\frac{{{a^3} + a + 1}}{3}} \right)\left( {\frac{{{b^3} + b + 1}}{3}} \right) \le \left( {\frac{{{a^3}{b^3} + ab + 1}}{3}} \right)\left| { \times \left( {\frac{{{c^3} + c + 1}}{3}} \right)} \right. > 0 \Rightarrow \\ \left( {\frac{{{a^3} + a + 1}}{3}} \right)\left( {\frac{{{b^3} + b + 1}}{3}} \right)\left( {\frac{{{c^3} + c + 1}}{3}} \right) \le \left( {\frac{{{a^3}{b^3} + ab + 1}}{3}} \right)\left( {\frac{{{c^3} + c + 1}}{3}} \right)\mathop \le \limits^{{\rm{Cebasev}}} \frac{{{a^3}{b^3}{c^3} + abc + 1}}{3} \le 1\\ {\rm{Ultima inegalitate este o consecinta a faptului}}\max \left\{ {abc} \right\} = 1. \end{array}

  26. sandy_sc
    maestru (V)

    ali wrote:
    \left(
    {\rm{Ultima inegalitate este o consecinta a faptului}}\max \left\{ {abc} \right\} = 1.
    \end{array}[/tex]


    Pt max{a,b,c}=1 egalitatea data pri enunt nu poate exista>In acest caz suma patratelor numerelor a,b,c este < 3

  28. ali
    maestru (V)

    Pt max{a,b,c}=1 egalitatea data pri enunt nu poate exista>In acest caz suma patratelor numerelor a,b,c este < 3


    Este defapt max{abc}=1 =/ max{a,b,c} (doar în anumite conditii sunt egale).
    Mai clar, din rel_1 si rel_2 => 27>=27abc <=> abc<=1.
    Sau, orice putere a lui abc <=1 => ultimul raport nu poate depăsi valoarea 1…. Fiind vorba de numere strict pozitive !

  29. Zeus
    veteran (III)

    Foarte bine lucrat. Am vrut si eu sa ma gandesc la ea ca a trezit unele controverse vad… dar nici n-am mai apucat 😀 WELL DONE!

Raspunde

Raspunde