Va rog sa ma ajutati la acest exercitiu.
Aratati ca (a+b+c)(1/a+1/b+1/c) ≥9 ,∇ a,b,c ∈R*
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Va rog sa ma ajutati la acest exercitiu.
Aratati ca (a+b+c)(1/a+1/b+1/c) ≥9 ,∇ a,b,c ∈R*
Eu cred ca este vorba despre multimea
Cred ca se stie ca in multimea
*** QuickLaTeX cannot compile formula: a+b+c \geq 3 \cdot \sqrt[3]{a \cdot b \cdot c *** Error message: File ended while scanning use of \next@. Emergency stop.*** QuickLaTeX cannot compile formula: a \cdot b+a \cdot c +b \cdot c \geq 3 \cdot \sqrt[3]{a \cdot b+a \cdot c+b \cdot c *** Error message: File ended while scanning use of \next@. Emergency stop..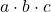
rezulta inegalitatea din problema ce trebuie de demonstrat.
Inmultind cele doua inegalitati si impartind prin produsul
Prea complicat inegrator …. problema se poate rezolva (cel mai simplu) cu MA-MG 3:
![\left\{ \begin{array}{l} a + b + c \ge 3\sqrt[3]{{abc}}\\ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \ge 3\sqrt[3]{{\frac{1}{{abc}}}} \end{array} \right. \Rightarrow \sum a \times \sum {\frac{1}{a}} \ge 9\sqrt[3]{{\frac{{abc}}{{abc}}}} = 9](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-fa2acb87b92291365fbb66a992209ea9_l3.png "Rendered by QuickLaTeX.com")
😀
Se poate si cu CBS_3 … iar foarte simplu