1)Sa se rezolve ecuatia in intervalul [-1,1] arcsin x +arcsin 1/radical din 2=pi/2
2)cos(2x+ pi/2)=cos(x-pi/2) in multimea R
3)3sin x+ radical din 3 cos x=0
4)cos 23pi/12 sin pi/12 (acest exercitiu l-am facut,dar babeste daca pot sa zic asa,exista vreo solutie mai rapida???
Daca puteti sa-mi dati niste formule si moduri practice de rezolvare la aceste exercitii
Si as mai avea niste nelamuriri,daca am facut corect acest gen de exercitiu
sinx+cosx=0 in intervalul [0,2pi)
am ridicat la patrat si mi-a dat
2sinxcosx=-1
am folosit formula 2sinxcosx=sin2x
sin2x=-1
si mi-a dat x={3pi/4,7pi/4}
O alta problema
sin3x=sinx in intervalul (0,pi)
mi-a dat
2sinxcos2x=0 => sinxcosx=0 acum aici ce fac??
sinx=0 si cosx=0 si fac o reuniune a rezultatelor sau o intersectie??
si arsin 0= 0 sau cu pi sau facem si 0 si pi? zic asta pentru ca
sin pi= sin 0 =0
daca m-ati putea ajuta sa-mi dati niste indicii privind aceste 2 exercitii
AM POSTAT EXERCITIILE LA CLASA A X-A.IMI CER SCUZE


1]. arcsin(1/(radical din 2))=pi/4 ->asc sin (x)=pi/2-pi/4=pi/4->x=1/(radical din 2).
2].2.x+pi/2=(+/-).(x-pi/2)-> determini pe x.
3]. 3.sin(x)+(radical din 3).cos(x)=0->(radical din 3).sin(x)+cos(x)=0->
tg(x)=-1/(radical din 3)->x=-pi/6 , sau x=5.(pi)/6. (ajunge pt .azi)
Demonstratie: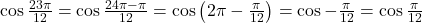 .
.
Din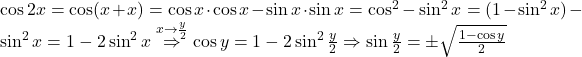 , semnul alegandu-se in functie de cadranul in care se afla unghiul de masura
, semnul alegandu-se in functie de cadranul in care se afla unghiul de masura  .
.
Punem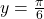 si cum unghiul
si cum unghiul 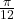 este in primul cadran, rezulta
este in primul cadran, rezulta 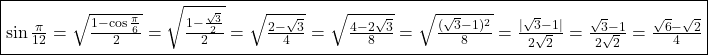 .
.
Din Formula fundamentala a trigonometriei, avem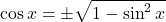 , unde semnul se alege dupa cadra. Cum
, unde semnul se alege dupa cadra. Cum 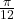 este in primul cadran, avem
este in primul cadran, avem 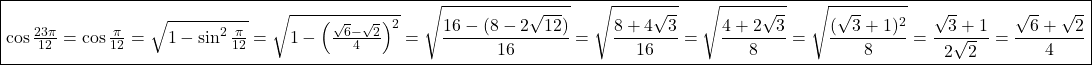 .
.
As avea o intrebare,ce formula ati aplicat aici cos(2pi-pi/12)=cos(pi/12)
Si raspunsul este gresit cos pi/12 *sin pi/12=1/2 cos pi/6*sin pi/6
Folosim formula sin2x=2sinxcosx
1/2 sin2pi/12=1/2 sin pi/6=1/2*1/2=1/4
Cand am facut babeste mi-a dat la fel.As vrea sa stiu decat acea formula care ati aplicat-o
La punctul 2) si 3) sunt mai multe solutii in functie de un parametru intreg k……
Va multumesc pentru raspuns,primul exercitiu l-am inteles.
Nu am inteles deloc exercitiul 2 si 3:|:|:|daca vreti sa le explicati mai detaliat
Va multumesc pentru raspuns,primul exercitiu l-am inteles.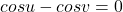 .Se aplica formula
.Se aplica formula 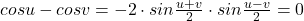 unde
unde 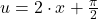 si
si 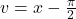 si rezulta in final solutiile
si rezulta in final solutiile 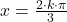 si respectiv
si respectiv 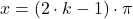 unde
unde 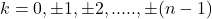
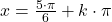 cu aceleasi valori pentru
cu aceleasi valori pentru  de mai sus.
de mai sus.
Nu am inteles deloc exercitiul 2 si 3:|:|:|daca vreti sa le explicati mai detaliat
2) Se trece membrul doi al ecuatiei in stanga si rezulta
3) Rezulta
Am folosit periodicitatea, iar apoi paritatea functiei cosinus.
Nu am observat faptul ca s-a copiat gresit enuntul problemei si de aceea am semnalat „greseala”(in caz, ca se mai uita cineva)🙂 :):)
Exercitiile de la punctele 2) si 3) rezolvate de mine s-au inteles?
Exercitiile de la punctele 2) si 3) rezolvate de mine s-au inteles?
Pe 2 l-am inteles,nu stiam ce sa fac ca nu aveam interval specificat,asa ca am lasat solutiile asa. si am facut intersectia lor .In acest caz solutiile coincid
x={=/- pi/4+ kpi}
Pe 3 l-am facut altfel,dar cred ca l-am gresit.Nu am inteles ce formula s-a aplicat.ma refer la tangenta:|:|nu am gasit cea formula:|:|
radical3 sin x- cos x=1 |:2
radical din 3/2 sin x – 1/2 cos x=1/2
am trasformat
cos pi/6 sinx-sin pi/6 cos x=1/2
sina cosb-sinb cosa=sin(a-b)
mi-a dat
sin(x-pi/6)=1/2
si mi-a dat x=((-1)^k*pi+pi+k)/6