Este o problemă la care eu nu vad rezolvarea. Cu siguranță este simpla. Putem presupune din prima ceea ce trebuie sa demonstram, ca sa vedem daca se verifica? 
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Ideea principala a acestei rezolvari nu imi apartine. Avem urmatorul desen:
Notam BC=a, AC=b, AB=c. Definim urmatoarele:
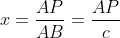
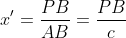
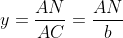
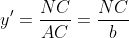
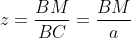
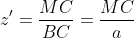
Din aceste relatii obtinem, in aceasta ordine:
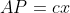
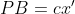
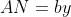
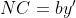
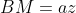
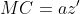
Observam ca) , deci
, deci 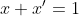 . Analog,
. Analog,  si
si  .
.
Pe de alta parte,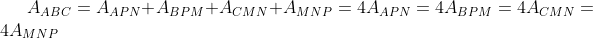 .
. , obtinem ca
, obtinem ca }2=4\frac{AP\cdot&space;AN\cdot\sin(PAN)}2) . Dar unghiurile BAC si PAN sunt unul si acelasi unghi, deci
. Dar unghiurile BAC si PAN sunt unul si acelasi unghi, deci 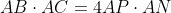 , de unde
, de unde 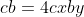 , si in final
, si in final 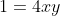 . Analog, obtinem
. Analog, obtinem 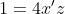 si
si 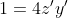 .
.
Din
Avem un sistem de 6 ecuatii cu 6 necunoscute:
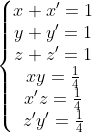
Din primele 3 ecuatii obtinem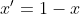 ,
, 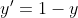 si
si 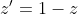 . Inlocuim in ultimele 2, care devin:
. Inlocuim in ultimele 2, care devin:
z=\frac14\\&space;(1-z)(1-y)=\frac14&space;\end{matrix}\right.)
Din prima ecuatie, avem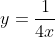 . Inlocuim in ultima ecuatie si le consideram acum doar pe ultimele 2:
. Inlocuim in ultima ecuatie si le consideram acum doar pe ultimele 2:
z=\frac14\\&space;(1-z)(1-\frac1{4x})=\frac14&space;\end{matrix}\right.)
Din prima ecuatie, avem}) . Inlocuim in ultima ecuatie, obtinem:
. Inlocuim in ultima ecuatie, obtinem:
})(1-\frac1{4x})=\frac14)
\cdot&space;4x) :
:
-1)(4x-1)=4x(1-x))
(4x-1)=4x-4x^2)
(4x-1)=4x-4x^2)
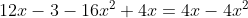
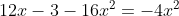
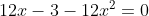

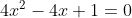
^2-2\cdot(2x)\cdot1+1=0)
^2=0)
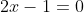
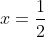
Inmultim cu
Impartim prin 3:
Din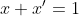 obtinem ca
obtinem ca 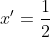 , din
, din  obtinem ca
obtinem ca 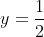 , iar din
, iar din 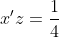 obtinem ca
obtinem ca 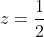 .
. , deci
, deci 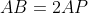 , deci P este mijlocul lui AB. Analog obtinem ca si celelalte puncte sunt mijloacele laturilor pe care se situeaza.
, deci P este mijlocul lui AB. Analog obtinem ca si celelalte puncte sunt mijloacele laturilor pe care se situeaza.
Dar