Am nevoie urgent pentru ca vreau sa invat ceva nou.
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Am nevoie urgent pentru ca vreau sa invat ceva nou.
Intr-un triunghi, daca o latura este mai mica decat cealalta, atunci si unghiurile opuse acestora au aceasta relatie. Acest lucru se poate demonstra cu ajutorul teoremei sinusurilor.
Deoarece D este mijlocul lui BC, avem ca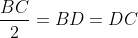
.
a)Din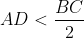
avem ca:
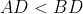⇒<m(\angle&space;BAD))
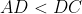⇒ <m(\angle&space;CAD))
Adunand cele 2 relatii obtinem:
+m(\angle&space;BCA)<m(\angle&space;BAD)+m(\angle&space;CAD))
Deoarece suma unghiurilor unui triunghi este 180 iar suma din partea dreapta a inegalitatii este chiar masura unghiului BAC obtinem ca:
<m(\angle&space;BAC))
)
)
>90)
b)Din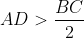
avem ca:
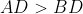⇒>m(\angle&space;BAD))
⇒ >m(\angle&space;CAD))
Adunand cele 2 relatii obtinem:
+m(\angle&space;BCA)>m(\angle&space;BAD)+m(\angle&space;CAD))
Deoarece suma unghiurilor unui triunghi este 180 iar suma din partea dreapta a inegalitatii este chiar masura unghiului BAC obtinem ca:
>m(\angle&space;BAC))
)
)
<90)