Doar E1,E2 si E3
va rog urgent,l
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Mai intai, cateva formule de combinatorica si explicatii:
Permutari:
Permutarile de n reprezinta numarul de moduri de rearanjare a unei multimi ordonate de n elemente. O alta definite este aceea ca o permutare este o functie bijectiva de la o multime la ea insasi. Numarul de permutari de n elemente(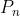
) este n factorial(notat n! si egal cu 1*2*3*..*n).
Aranjamente:
Aranjamentele de n luate cate k reprezinta numarul de moduri de a lua k elemente, dintr-o multime de n, in care ordinea elementelor conteaza(adica (a, b) este diferit de (b, a)). O alta definitie a aranjamentului de n luate cate k este ca acesta este numarul de functii injective dintr-o multime de k elemente la o multime de n elemente. Numarul de aranjamente de n elemente luate cate k este notat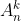
si este egal cu 
.
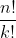Combinari:
Combinarile de n luate cate k reprezinta numarul de moduri in care putem alege k elemente din n,in care ordinea elementelor nu conteaza(adica, spre deosebire de aranjamente, (a, b) este acelasi lucru cu (b, a)). Altfel spus, numarul de combinari de n luate cate k este numarul de submultimi de k elemente ale unei multimi de n elemente. Numarul de combinari de n luate cate k se noteaza cu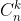
si este egal cu !})
.
E1.Folosim formulele descrise mai sus.
E2.a)!}-5!}{\frac{5!}{(5-2)!}}=\frac{\frac{7!}{3!}-5!}{\frac{5!}{3!}}=\frac{\frac{5040}{6}-120}{\frac{120}{6}}=\frac{840-120}{20}=\frac{720}{20}=36)
b)!}}{5*5!-3!}=\frac{2*6+3*\frac{4!}{2!}}{5*120-6}=\frac{12+3*\frac{24}{2}}{600-6}=\frac{12+3*12}{594}=\frac{12+36}{594}=\frac{48}{594}=\frac{8}{99})
c)!}-\frac{11!}{(11-5)!}}{\frac{10!}{(10-5)!}-\frac{10!}{(10-4)!}}=\frac{\frac{11!}{11!}-\frac{11!}{6!}}{\frac{10!}{5!}-\frac{10!}{6!}}=\frac{1-7*8*9*10*11}{6*7*8*9*10-7*8*9*10}=\frac{1-55440}{30240-5040}=\frac{-55439}{25200})
d)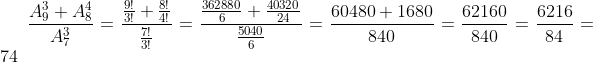
E3.Consideram primul examen. Acesta poate fi programat in oricare din cele 15 zile. Avem deci 15 variante pentru acesta. Dupa ce il programam, raman 14 variante(zile) pentru celelalte examene. In acelasi mod, avem 14 variante pt al 2-lea, 13 pentru al 3-lea, 12 pentru al 4-lea si 11 pentru ultimul. In total, avem 15*14*13*12*11=360360.
O alta metoda este sa observam ca trebuie sa alegem 5 elemente(zilele in care se dau examene) dintr-o multime de 15 elemente(totalul de zile), contand ordinea in care alegem. Aceasta este chiar definitia aranjamentelor, deci numarul cautat este:
Daca primul examen se da in prima zi, mai avem de ales zile pentru celelalte 4 examene. Deoarece prima zi este ocupata, ne raman 14 zile. Rationand ca mai inainte, obtinem ca numarul de posibilitati este: