Home/ Intrebari/Q 93121
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

Garfield3090
Pe: 2019-07-19T09:11:35+03:00 In: In:

Polinom admitere

Se dă polinomul f=5X^3-aX^2-aX+5, cu a \in \mathbb{R} și având rădăcinile x_1, x_2, x_3 \in \mathbb{C}.
a) Calculați f(-1)
b) Determinați a \in \mathbb{R} pentru care polinomul f are toate rădăcinile reale.
c) Determinați a \in \mathbb{R} pentru care | x1 | + | x2 | + | x3 |=3.

Primele două subpuncte le-am făcut, la b) am obținut descompunerea:
f = (X+1)(5X^2-(a+5)X+5) , iar de la punctul a) știu că x1 este rădăcină a polinomului f, deci | x1 | = | -1 | = 1.
La c), rezultă că | x2 | + | x3| = 2. Am lucrat cu ecuația 5x^2-(a+5)x+5 = 0 și i-am scris relațiile lui Viete:
x_2 + x_3 = \frac{a+5}{5}
x_2 x_3 = 1
De aici, am încercat să egalez pe x2 + x3 cu suma modulelor și am obținut ecuația \frac{a+5}{5} = 2 de unde rezultă că a = 5. În barem scrie că a \in \left \{-15,5 \right \}. Cum s-a aflat cea de a doua soluție a lui a? Menționez că am încercat diferite abordări, dar nu-mi iese rezolvarea.
Vă mulțumesc anticipat.

Similare

2 raspunsuri

  1. Felixx
    veteran (III)

    Din x_{2}x_{3}=1 ,trecand la modul avem:
    \left | x_{2} \right |\cdot \left | x_{3} \right |=1
    si cum
    \left | x_{2} \right |+\left | x_{3} \right |=2
    \left | x_{2} \right |si\left | x_{3} \right | sunt solutiile ecuatiei in z :
    z^{2}-Sz+P=0\Rightarrow \left ( z-1 \right )^{2}=0\Rightarrow z_{1}=z_{2}=1\Rightarrow \left | x_{2} \right |=1,\left | x_{3} \right |=1\Rightarrow x_{2}=\pm 1,x_{3}=\pm 1\Rightarrow x_{2}+x_{3}=-2,x_{2}+x_{3}=2\Rightarrow a=-15,a=5
    OBS.
    Cazul x_{2}=-1,x_{3}=1 si invers nu poate avea loc ,deoarece din
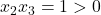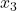    x_{2}x_{3}=1>0 rezulta ca x_{2} si x_{3} au acelasi semn (ambele pozitive sau ambele negative)

  2. Garfield3090

    Mulțumesc mult!

Raspunde

Raspunde