Home/ Intrebari/Q 77893
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

gefest
Pe: 2012-09-06T18:35:53+03:00 In: In:

limita integralei

Sa se calculeze \lim_{x\to 0}\frac{\int_0^x\left(\sqrt[3]{1+6x^4}-1\right)\mathrm{dx}}{x^5}.

Vreau sa ajung la nedeterminarea \frac00. Dar nu stiu cum se calculeaza limita numaratorului: \lim_{x\to 0}\int_0^x\left(\sqrt[3]{1+6x^4}-1\right)\mathrm{dx}.

Similare

5 raspunsuri

  1. gefest

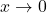    Incerc asa: 0\leq\sqrt[3]{1+6t^4}-1\leq 1+6t^4. Integrez \int_0^x. Iau limita (cind x\to 0) si folosesc teorema clestelui.

  2. DD
    profesor

    Integrala definita data o vom scrie ; F(x)-F(0) , unde F(x) este primitiva integralei nedefinite. Vom scrie limita sub forma;
    L=lim(x->0) din [{(F(x)-F(0))/x}.{1/x^4}].Conf teoremei lui Lagrange, factorul ; lim(x->0) din [{F(x)-F(0)}/x]=lim(x->0) din [(al 3-a radical din [(1+6.X^4))-1] , deci L=lim(x->0) din [{( al 3-a radical din (1+6.x^4))-1}/x^4]. Limita fiind de tipul 0/0, aplicam L’Hospital; Deci;
    L=lim(x->0) din [(1/3).(24.x^3)./{4.x^3.(al 3-a radical din (1+6.x^4))}=2

  4. gefest

    Raspunsul este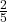 \frac25.

  5. DD
    profesor

    Ai dreptate. Folosirea teoremei lui Lagrange numai aproximeaza limita. De fapt (F(x)-F(0))/x =F'(c)=f(c)=(al 3-a radical din (1+6.c^4)) – 1 , unde ; 0<c<x si eu am aproximat pe c=x , cand x->0 , ori aproximatia este grosolana.
    Facem altceva , Cum si aceasta limita este de tipul 0/0 , aplicam L’Hospital. Tinem seama ca integrala I(x) derivata , este egala cu functia ce trebue integrata. deci ; lim(x->0) din (I(x))’/(5.x^4)=(1/5).lim(x->0) din [{(al 3-a radical din (1+6.x^4)) – 1}/x^4] Si aceasta limita este de tipul 0/0 si aplicam din nou L”Hospital si aceasta devine ; (1/5).lim(x->0) din [(1/3).24.x^3./{4.x^3.(al 3-a radical din (1+6.x^4)^2)]=2/5 Scuze! Se vede ca-mi place teorema lui Lagrange.

  6. Integrator
    maestru (V)

    gefest wrote: Sa se calculeze \lim_{x\to 0}\frac{\int_0^x\left(\sqrt[3]{1+6x^4}-1\right)\mathrm{dx}}{x^5}.

    Vreau sa ajung la nedeterminarea \frac00. Dar nu stiu cum se calculeaza limita numaratorului: \lim_{x\to 0}\int_0^x\left(\sqrt[3]{1+6x^4}-1\right)\mathrm{dx}.


    Daca x\to 0 atunci inseamna ca acea integrala simpla definita care este de fapt o suprafata ce tinde la zero si cum si numitorul tinde la zero inseamna ca este cazul \frac{0}{0} si se poate aplica regula lui L’Hospital.Considerand ca valoarea integralei este F(x) atunci F'(x)=\sqrt[3]{1+6x^4}-1 si in concluzie acea limita devine L=\lim_{x\to 0}\frac{\sqrt[3]{1+6x^4}-1}{x^5} si aplicand o singura data L’Hospital rezulta imediat ca valoarea limitei este L=\frac{8}{20}=\frac{2}{5}.

Raspunde

Raspunde