Sa se rezolve urmatoarele ecuatii exponentiale:
![Rendered by QuickLaTeX.com \[ \begin{array}{l} A).\quad 3^{\sqrt {x - 2} } + 5^{\sqrt {x^2 - 3x + 2} } = 1 \\ B).\quad a^{2x} + b^{2x} + 2(ab)^x = 0\quad ,cu\;a,b > 0,\;a,b \ne 1 \\ C).\quad 6^x - 2^x = 32 \\ D).\quad 2^x - \left( {\frac{3}{5}} \right)^x = \frac{7}{5} \\ \end{array} \]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-939fd596604568e166c8fb192792255f_l3.png)
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
B)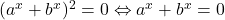 . Dar
. Dar 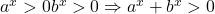 , adica ecuatia nu are solutii reale.
, adica ecuatia nu are solutii reale.
D)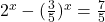
Functia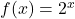 este strict crescatoare (exponentiala cu baza supraunitara)
este strict crescatoare (exponentiala cu baza supraunitara)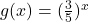 este strict descrescatoare (exponentiala cu baza subunitara)
este strict descrescatoare (exponentiala cu baza subunitara) 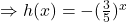 strict crescatoare.
strict crescatoare.
Functia
Adica in membrul drept avem o functie strict crescatoare [suma a doua functii strict crescatoare] ( si deci injectiva ), iar in membrul stang avem o constanta. Ecuatia are deci cel mult o solutie. Observam ca verifica si deci aceasta este singura.
verifica si deci aceasta este singura.
C)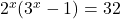
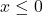 atunci
atunci 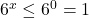 si
si 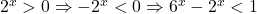 adica nu avem solutii.
adica nu avem solutii. avem
avem 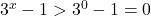 adica in membrul drept al ecuatiei avem un produs de functii strict crescatoare si pozitive, care este si el la randul lui o functie strict crescatoare (si deci injectiva)
adica in membrul drept al ecuatiei avem un produs de functii strict crescatoare si pozitive, care este si el la randul lui o functie strict crescatoare (si deci injectiva)  ecuatia are solutie unica. Observand
ecuatia are solutie unica. Observand  solutie, aceasta este unica.
solutie, aceasta este unica.
Daca
Pentru
A) Se pun conditiile de existenta pentru cei doi radicali (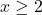 si
si ![Rendered by QuickLaTeX.com x\in(-\infty,1]\cup[2,\infty)](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-da03724b028c4d4ed9d5a8f0798ae591_l3.png)
 [tex]x\geq 2[/tex]). Observam ca
[tex]x\geq 2[/tex]). Observam ca 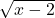 este functie strict crescatoare (compunere dintre functia radical de ordinul doi si functia de gradul intai cu coeficient dominant pozitiv,ambele strict crescatoare). De asemenea, deoarece in cazul functiei de gradul doi de sub al doilea radical avem
este functie strict crescatoare (compunere dintre functia radical de ordinul doi si functia de gradul intai cu coeficient dominant pozitiv,ambele strict crescatoare). De asemenea, deoarece in cazul functiei de gradul doi de sub al doilea radical avem 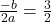 si
si 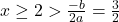 , functia de gradul doi este strict crescatoare pentru
, functia de gradul doi este strict crescatoare pentru 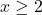 si rezulta ca si
si rezulta ca si 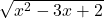 este strict crescatoare (compunere dintre functia radical (crescatoare) de ordinul doi si functia de gradul doi restrictionata pentru a fi strict crescatoare). Cum
este strict crescatoare (compunere dintre functia radical (crescatoare) de ordinul doi si functia de gradul doi restrictionata pentru a fi strict crescatoare). Cum 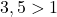 , avem in membrul stang al ecuatiei suma de functii strict crescatoare, adica functie strict crescatoare. Dar atunci
, avem in membrul stang al ecuatiei suma de functii strict crescatoare, adica functie strict crescatoare. Dar atunci 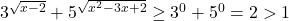 , adica ecuatia nu are solutii reale.
, adica ecuatia nu are solutii reale.
Multumesc!🙂
Cu cea mai mare placere!
EDIT: Am gresit la ultima problema. De fapt ecuatia nu are solutii. Am editat celalalt post. Imi cer scuze!