Home/ Intrebari/Q 73605
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

andrei_g
Pe: 2011-10-01T10:56:08+03:00 In: In:

Inegalitate din R

Daca a si b sunt numere reale strict pozitive, sa se arate ca:

    \[ \frac{8}{{(\sqrt a + \sqrt b )^2 }} \le \frac{2}{{\sqrt {ab} }} \le \frac{1}{a} + \frac{1}{b} \]

Multumesc!

Similare

41 raspunsuri

  1. J3anina
    maestru (V)

    Pentru inegalitatea din stanga folosesti faptul ca produsul mezilor=produsul extremilor si apoi vei obtine faptul ca: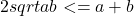 2sqrt{ab}<=a+b, care se demonstreaza folosind: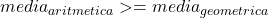 media_{aritmetica}>=media_{geometrica}

    Pentru inegalitatea din dreapta se foloseste faptul ca: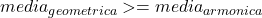 media_{geometrica}>=media_{armonica}

    Daca nu reusesti, nu ezita sa revii cu intrebari.

  2. andu_flavius95
    maestru (V)

    O alta metoda pt. inegalitatea a 2 este ma>=mg:

        \[ \frac{1}{a} + \frac{1}{b} \ge 2\sqrt {\frac{1}{{ab}}} = \frac{2}{{\sqrt {ab} }} \]

  4. andrei_g

    Multumesc mult! Iar la prima inegalitate nu se poate aplica ceva cu inegalitatea mediilor?(profesoara ne-a dat aceasta indicatie la scoala).

  5. J3anina
    maestru (V)

    Da da, exact asta am spus mai sus.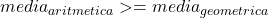
    Se aplica inegalitatea mediilor si anume: media_{aritmetica}>=media_{geometrica}
    dar se aplica doar dupa ce faci produsul mezilor=produsul extremilor, pentru ca ti se va mai simplifica calculul (imi cer scuze pentru cacofonie). :d

  6. andrei_g

    Eu asa am facut cu inegalitatea mediilor

        \[ \frac{8}{{a + b + 2\sqrt {ab} }} \le \frac{8}{{a + b + a + b}} = \frac{4}{{a + b}} \]

    dar cum fac mai departe… deoarece iasa chiar invers…

    Nu am facut calculul direct deoarece ma gandesc poate merge dedusa relatia cum am facut mai sus. 🙂

  8. J3anina
    maestru (V)

    Tu stii ce inseamna inegalitatea mediilor?

    Care parte din aceast inegalitate ai folosit-o tu aici?

  9. andrei_g

    Am folosit faptul ca 2sqrt(ab)<=a+b

  10. J3anina
    maestru (V)

    Este adevarat ce spui, dar de unde stii asta?

  12. andrei_g

    Din faptul ca media aritmetica >= media geometrica.

  13. J3anina
    maestru (V)

    Perfect!

    Dar daca eu ti-am zis sa efectuezi prima data produsul mezilor = produsul extremilor, de ce nu m-ai ascultat?

    Incearca sa faci asta si apoi aplici ma>=mg.
    Este mult mai usor!

  14. J3anina
    maestru (V)

    \frac{8}{(\sqrt{a}+\sqrt{b})^{2}}\leq\frac{2}{\sqrt{ab}}

    Facand produsul mezilor = produsul extremilor vei obtine:

    8sqrt{ab}\leq2(a+b+2\sqrt{ab}) \Rightarrow 4\sqrt{ab} \leq2a+2b\Rightarrow2\sqrt{ab}\leq a+b

    Acum poti aplica inegalitatea mediilor si anume: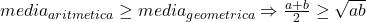 media_{aritmetica}\geq media_{geometrica}\Rightarrow\frac{a+b}{2}\geq\sqrt{ab} de unde iti rezulta inegalitatea dorita.

  16. andrei_g

        \[ 8\sqrt {ab} \le 2a + 2b + 4\sqrt {ab} = > 2a + 2b - 4\sqrt {ab} \ge 0 = > (\sqrt a - \sqrt b )^2 \ge 0 \]

    Asa este bine?

  17. J3anina
    maestru (V)

    Daca eu ti-am scris rezolvarea mai sus, tu de ce mai intrebi daca este bine?

  18. andrei_g

    Scuze, dar cand am scris nu era afisata. In momentul scriam rezolvarea.

  20. J3anina
    maestru (V)

    andrei_g wrote:

        \[ 8\sqrt {ab} \le 2a + 2b + 4\sqrt {ab} = > 2a + 2b - 4\sqrt {ab} \ge 0 = > (\sqrt a - \sqrt b )^2 \ge 0 \]

    Asa este bine?


    Este bine si asa, doar ca folosind aceasta metoda, nu vei mai avea nevoie de inegalitatea mediilor.

  21. andu_flavius95
    maestru (V)

    J3anina, nu-i reprosa acestui user neatentie si alte chestii, vad ca incearca si doar intreaba sa stie daca-i bine.Nu cred ca vrea doar sa-i faci tema, vrea sa si inteleaga 🙂

  22. J3anina
    maestru (V)

    Asa este, ai dreptate! Cred ca am fost putin cam dura! 🙂

    Important este ca a inteles (sunt sigura de asta)!

  24. andu_flavius95
    maestru (V)

    O alta metoda, cu inegalitatea mediilor:
    Prima inegalitate este <=> cu :

        \[ \begin{array}{l} \frac{{\sqrt {ab} }}{{a + b + 2\sqrt {ab} }} \le \frac{2}{8} = \frac{1}{4} \\ Avem\;\frac{{\sqrt {ab} }}{{a + b + 2\sqrt {ab} }} \le \frac{{\frac{{a + b}}{2}}}{{a + b + a + b}} = \frac{{a + b}}{2} \cdot \frac{1}{{2(a + b)}} = \frac{1}{4} \\ \end{array} \]

    este adevarat. 🙂

  25. andu_flavius95
    maestru (V)

    Ce zici,J3anina ,este mai buna aceasta metoda cu inegalitatea mediilor decat cea cu efectuarea calculelor?

  26. J3anina
    maestru (V)

    Destul de interesanta, dar la nivel de clasa a IX-a sau a X-a mi se pare mult mai abordabila cea folosita de mine.
    Oricum, orice explicatie ori metoda in plus este bine venia!

  28. andu_flavius95
    maestru (V)

    Bine atunci dar si aceasta metoda este tot de clasa 9 sau 10 😀

  29. J3anina
    maestru (V)

    Ai dreptate, este de clasa IX, X, dar mi se pare mai greu de observat.
    Oricum, foarte bine ca ai postat aceasta idee.

  30. DD
    profesor

    1]. [(radical din a)+(radical din b)]/2>=(al 4-a radical din (ab)) ->
    4/[((radical din a)+(radical din b))^2]<=1/(radical din (a.b))
    2]. (1/a+1/b)/2>=1/(radical din (a.b))
    3]. 1/a+1/b>=2/(radical din (a.b))>=8/[(radical din a)+(radical din b)]^2

  32. andu_flavius95
    maestru (V)

    DD wrote: 1]. [(radical din a)+(radical din b)]/2>=(al 4-a radical din (ab)) ->
    4/[((radical din a)+(radical din b))^2]<=1/(radical din (a.b))
    2]. (1/a+1/b)/2>=1/(radical din (a.b))
    3]. 1/a+1/b>=2/(radical din (a.b))>=8/[(radical din a)+(radical din b)]^2

    Nu stiu ce rol mai au acum raspunsuri, dar n-ar fi rau un program de latex, ii cam greu de urmarit…

  33. PhantomR
    expert (VI)

    andu_flavius95 wrote: O alta metoda, cu inegalitatea mediilor:
    Prima inegalitate este <=> cu :

        \[ \begin{array}{l} \frac{{\sqrt {ab} }}{{a + b + 2\sqrt {ab} }} \le \frac{2}{8} = \frac{1}{4} \\ Avem\;\frac{{\sqrt {ab} }}{{a + b + 2\sqrt {ab} }} \le \frac{{\frac{{a + b}}{2}}}{{a + b + a + b}} = \frac{{a + b}}{2} \cdot \frac{1}{{2(a + b)}} = \frac{1}{4} \\ \end{array} \]

    este adevarat. 🙂

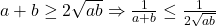    Daca a,b>0, , a+b \geq 2\sqrt{ab} \Rightarrow \frac{1}{a+b}\leq \frac{1}{2\sqrt{ab}} (se schimba semnele), deci primul pas al rezolvarii este gresit.

  34. andu_flavius95
    maestru (V)

    Presupunem prin absurd ca ai dreptate, insa cum demonstrezi acest lucru ❓ 🙂

    Contraexemplu:
    daca avem:

        \[ \frac{7}{3} \ge \frac{6}{5} \Rightarrow \frac{5}{3} \ge \frac{6}{7} \]

  36. PhantomR
    expert (VI)

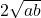    Nu e nimic de presupus, e un adevar.. Inmulteste relatia mea cu a+b sau 2\sqrt{ab} (ambele pozitive) si obtii inegalitatea mediilor 🙂.

    Un exemplu concret:

    3<5 \Rightarrow \frac{1}{3} > \frac{1}{5}.

  37. andu_flavius95
    maestru (V)

    Deci, vrei sa spui ca numitor nu se accepta inegalitatea mediilor?

  38. PhantomR
    expert (VI)

    Ba da, dar se schimba semnele..

  40. andu_flavius95
    maestru (V)

    Tu ai vreo metoda de rezolvare pt. problema care nu necesita interschimbare in proportie? Ceva cu inegalitatea mediilor..

  41. PhantomR
    expert (VI)

    Nu, nu am. In legatura cu acel contraexemplu din postul anterior (pe care nu l-am observat si imi cer scuze!), nu prea vad ce legatura are cu afirmatia mea.

    Ca sa ma asigur ca ai inteles ce am vrut sa spun si sa nu fiu interpretat rau:

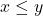    Fie x,y>0 cu x \leq y. Impartim inegalitatea prin 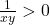\frac{1}{xy}>0 si obtinem 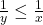\frac{1}{y}\leq \frac{1}{x} sau scris invers \frac{1}{x}\geq \frac{1}{y}.

  42. andu_flavius95
    maestru (V)

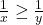    Ok, iti dau dreptate 🙂 si as avea o intrebare: ai prins olimpiade balcanice sau internationale?

  44. PhantomR
    expert (VI)

    Imi cer scuze daca am fost prea dur! 🙁 Nu asta a fost intentia mea, ci doar aceea de a face o mica observatie care s-ar putea sa iti foloseasca alta data.

    Balcanice? Internationale? Aualeu, nu! Sunt doar un mic prostanac 😆.. cum sa ajung pana acolo.

  45. andu_flavius95
    maestru (V)

    Atunci, care a fost cea mai avansata faza de olimpiada la care ai fost?

  46. PhantomR
    expert (VI)

    Am prins si eu o nationala.. dar doar din noroc. E nevoie de mult exercitiu pentru a realiza ceva la matematica.. sa nu mai vorbim de talent si mie imi lipsesc ambele.

    As dori sa iti adresez si eu aceeasi intrebare, caci am vazut ca esti foarte activ pe forum si dai multe solutii interesante.

  48. andu_flavius95
    maestru (V)

    Eu am prins multe olimpiade locale, si o singura data am mers la cea judeteana 🙂

    Oricum, poate anul o sa am mai multe sanse.. De la ultima olimpiada am muncit in continuu…mi-am marit cunostiintele si dezvoltat alte idei de rezolvare/

  49. PhantomR
    expert (VI)

    Esti pe drumul cel bun! Continua sa muncesti din greu si sigur vei reusi! Ca un sfat, sa nu uiti totusi de celalalte materii de sutiu de la scoala! 😀

    Iti doresc multa bafta la olimpiada si la scoala!:)

  50. andu_flavius95
    maestru (V)

    Nu , nu am uitat si nu o sa uit niciodata de celelalte materii de scoala. Si ele sunt importante, sunt activ si la ele ,mai muncesc si la ele cand am timp.

    Multumesc mult! Si bafta si tie 😀 .Poate ne vom intalni anul acesta la vreo olimpiada///

  52. PhantomR
    expert (VI)

    Ma bucur mult sa aud acest lucru!

    Multumesc mult si eu! Sa fie! Sper si eu sa ne vedem!:D:D

  53. andu_flavius95
    maestru (V)

    Asa sa fie! Sa dea Domnul sa pice exercitii cat mai accesibile si usor de abordat 😀

  54. PhantomR
    expert (VI)

    Doamne ajuta! 🙂

Raspunde

Raspunde