Ex 3 va rog!
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Demonstram implicatia directa, anume ca daca N este mijlocul lui CD, atunci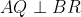 . Avem urmatorul desen:
. Avem urmatorul desen: 
QE este perpendiculara pe AB, iar T este punctul de intersectie al AQ si BR. Notam lungimea laturii patratului cu l.
Deoarece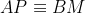 , rezulta ca
, rezulta ca 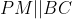 , deci unghiurile triunghiurilor PAR si DAN sunt congruente, adica triunghiurile sunt asemenea. Atunci:
, deci unghiurile triunghiurilor PAR si DAN sunt congruente, adica triunghiurile sunt asemenea. Atunci:
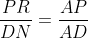
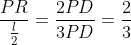
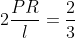
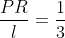
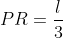
Analog,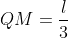 . Deoarece
. Deoarece 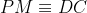 , rezulta ca
, rezulta ca 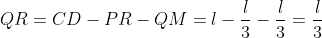 .
.
Aplicam teorema lui Pitagora in triunghiul QAE. Folosim faptul ca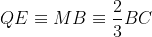 , precum si
, precum si 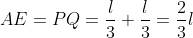 :
:

^2+(\frac{2}{3}l)^2=AQ^2)
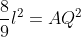
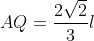
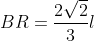
Analog,
Deoarece RQ||AB, unghiurile triunghiurilor TAB si TQR sunt congruente, deci triunghiurile sunt asemenea. Atunci:

 , adica
, adica 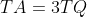 si
si 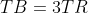 , sau
, sau 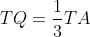 si
si 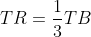 . Atunci:
. Atunci:
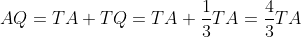
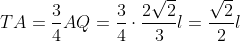 .
.
Rezulta ca
Analog obtinem ca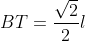 .
.
In final, observam ca^2+(\frac{\sqrt2}{2}l)^2=\frac24l^2+\frac24l^2=l^2=AB^2) , deci din Teorema lui Pitagora, triunghiul TAB este dreptunghic in T.
, deci din Teorema lui Pitagora, triunghiul TAB este dreptunghic in T.
Demonstram acum si inversa, adica daca unghiul ATB este drept, atunci N este mijlocul lui CD.
Folosim acelasi desen ca mai sus. Notam lungimea lui DN cu n. Atunci lungimea lui NC este l-n.
Deoarece PQ||DC, unghiurile triunghiurilor DAN si PAQ sunt congruente, deci triunghiurile sunt asemenea. Atunci:
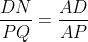
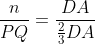
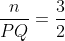
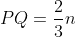
Analog, din asemanarea triunghiurilor BCN si BMR, obtinem:
)
Aplicam Teorema lui Pitagora in triumghiurile QTA si RTB:
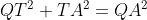
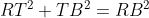
Adunam cele 2 relatii:
+(TA^2+TB^2)=QA^2+RB^2)
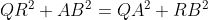
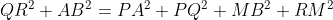
Deoarece triunghiurile QTR si ATB sunt dreptunghice:
Deoarece PQA su MRB sunt dreptunghice, relatia devine:
Inlocuim valorile(in functie de l si n) pe care le-am calculat mai sus:
^2+l^2=(\frac23l)^2+(\frac23n)^2+(\frac23l)^2+(\frac23(l-n))^2)
Inmultim cu 9:
Impartim cu 2 si inversam membrul stang cu membrul drept: