 tema matematica det
tema matematica det
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
1.-6\cdot(-2)=-12+12=0)
2.Din teorema lui Hamilton-Cayley, stim ca pentru orice matrice A de 2×2 are loc relatia:
A-(4-2\cdot3)I_2=5A+2I_2)
=\det(5A+2I_2-2A-I_2)=\det(3A-I_2)=\det(\begin{pmatrix}&space;12&9\\6&3&space;\end{pmatrix}-I_2)=\det\begin{pmatrix}11&9\\6&2\end{pmatrix}=2*11-6*9=22-54=-32)
Inlocuind, obtinem:
3.=\det(\begin{pmatrix}&space;-1&2&2\\2&2&-1&space;\end{pmatrix}\cdot&space;\begin{pmatrix}-1&2\\2&2\\2&-1\end{pmatrix})=\det(\begin{pmatrix}9&0&9\end{pmatrix})=9\cdot9=81)
4.Adunam ultima linie peste prima, apoi dezvoltam in functie de prima linie:
\cdot(-1)^{1+2}\begin{vmatrix}-1&-1\\-1&1\end{vmatrix}=2(-1-1)=-4)
5.Dezvoltam dupa prima linie:
^{1+1}(x-1)+1\cdot(-1)^{1+2}(1-x)+x\cdot(-1)^{1+3}(1-x)=x-1-(1-x)+x(1-x)=x-1-1+x+x-x^2=-x^2+3x-2=-(x^2-3x+2)=-(x-1)(x-2))
Produsul este 0 daca cel putin unul dintre termeni este egal cu 0, deci avem solutiile 1 si 2.
6.-5(x+3)=-6x+x+1)
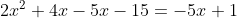
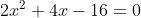
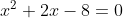
Solutiile sunt -4 si 2(din relatii lui viete, -4+2=-2 si -4*2=8).
7.+\det(AB)=\det(A+B)+\det(A)\cdot\det(B)=\begin{vmatrix}7&-2\\4&6\end{vmatrix}+(14+6)(-5-2)=42-(-8)+20\cdot-7=42+8-140=50-140=-90)