Salut.Exercitiul A3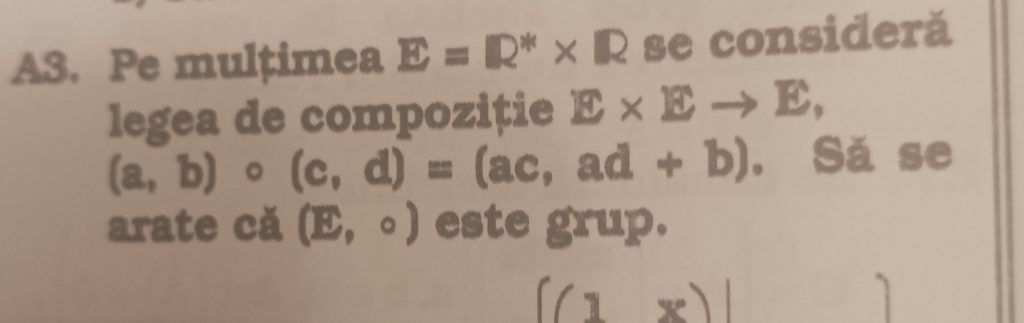
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
E clar că mulțimea E este parte stabilă.
![[(a,b)\circ(c,d)]\circ(e,f)=(ac,ad+b)\circ(e,f)=(ace,acf+ad+b)](https://latex.codecogs.com/gif.latex?[(a,b)\circ(c,d)]\circ(e,f)=(ac,ad+b)\circ(e,f)=(ace,acf+ad+b))
![(a,b)\circ[(c,d)\circ(e,f)]=(a,b)\circ(ce,cf+d)=(ace,acf+ad+b)](https://latex.codecogs.com/gif.latex?(a,b)\circ[(c,d)\circ(e,f)]=(a,b)\circ(ce,cf+d)=(ace,acf+ad+b))
)
elementul neutru. Trebuie ca \circ(e_1,e_2)=(e_1,e_2)\circ(a,b)=(a,b),&space;\&space;\forall&space;(a,b)\in&space;E)
=(a,b)\Rightarrow&space;ae_1=a,&space;\&space;ae_2+b=b\Rightarrow&space;a=1,b=0)
\circ(a,b)=(a,b))
, deci elementul neutru este perechea )
.\in&space;E,&space;\&space;\exists&space;(x,y)\in&space;E)
astfel încât \circ&space;(x,y)=(x,y)\circ(a,b)=(1,0))
\circ(x,y)=(1,0))
rezultă =(1,0)\Rightarrow&space;ax=1,&space;\&space;ay+b=0\Rightarrow&space;x=\dfrac{1}{a},&space;\&space;y=-\dfrac{b}{a})
\circ(a,b)=(1,0))
)
este )
.)
este grup
Demonstrăm distributivitatea. Calculăm cei doi membri ai relației de distributivitate:
Cum rezultatele sunt egale, rezultă că legea este distributivă.
Elementul neutru. Fie
Rezultă
Prin calcul se verifică și
Elemente simetrizabile. Trebuie ca pentru orice
Din
Prin calcul se verifică și egalitatea
Deci simetricul lui
În concluzie,