![]()
Am încercat sa scriu expresia din interiorul integralei ca ![]() și așa să încerc să „prind” în clește; nu a funcționat.
și așa să încerc să „prind” în clește; nu a funcționat.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Calculele sunt destul de laborioase in rezolvarea acestei probleme.O sa schitez pasii necesari.

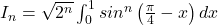 .Aici facem substitutia de variabila :
.Aici facem substitutia de variabila : 

 si
si  .Atunci:
.Atunci:
 , care este o relatie de recurenta ce se obtine facand o simpla integrare prin parti
, care este o relatie de recurenta ce se obtine facand o simpla integrare prin parti
Atunci:
Integrala devine:
Atentie la limitele de integrare la calculul acestei integrale! Ce modalitate ai de a o scrie altfel?
De asemenea in aceasta faza poti folosi rezultatul:
Fie
Efectuand calculele ( foarte multe) vei obtine relatia de recurenta pentru sirul din cazul problemei tale.Vei trece apoi la limita in relatia de recurenta
tinand seama de :
Vă mulțumesc!
Poate te ajuta la admitere:


Soluția de mai sus, a lui Felixx, este una particulară care se bazează pe faptul că în integrală apare funcția trigonometrică g(x)=cosx-sinx. Pentru altă funcție, trebuie găsita altă rezolvare. să scriu o demonstrație mai generală, valabilă pentru o clasă mai largă de șiruri de integrale, dar nimeni nu s-a arătat interesat. Eu aș propune să utilizam următorul rezultat: Dacă
să scriu o demonstrație mai generală, valabilă pentru o clasă mai largă de șiruri de integrale, dar nimeni nu s-a arătat interesat. Eu aș propune să utilizam următorul rezultat: Dacă ![Rendered by QuickLaTeX.com a\in (-1;1),\;f:[a;1]\to \mathbb{R}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-bd604a94bc103eb80ee56d3393873a68_l3.png) este derivabilă și cu derivată continuă, atunci
este derivabilă și cu derivată continuă, atunci

 .
.
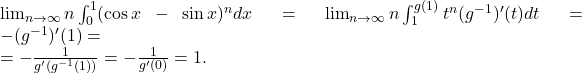
 pentru că g(0)=1.
pentru că g(0)=1.
Eu m-am oferit aici
De fapt cred că rezultatul este valabil și pentru funcții f doar cuntinue pe intervalul respectiv, dar mi-e mai greu de demonstrat.
g'(x)=-sinx-cosx<0 pe [0; 1] arată că g este strict descrescătoare pe [0; 1], deci g:[0; 1]–>[g(1); 1] este inversabilă și inversa sa este derivabilă ori de câte ori este derivabilă g. În plus, din pi/4<1<pi/2: g(pi/2)<g(1)<g(pi/4), adică -1<g(1)<0.
Propun schimbarea de variabilă t=g(x), deci
Foarte interesant rezultatul dumneavoastra si util in acelasi timp.
V-as intreba daca putem sa-l aplicam si in cazul limitei de mai jos(si daca se poate sa detailati putin) sau daca exista o alta abordare mai simpla:
stiind ca intervalul de integrare
………………………………………………………………………………………………………
Eu am incercat asa :
Din
Atunci conform criteriul clestelui limita ar fi zero.
Pentru a calcula ultima limita, am urmat pasii expusi mai sus in cazul problemei UTCN2015/12, ce mi-a luat ceva timp de finalizare a calculelor.
MULTUMESC.
Observ. Această inegalitate poate fi falsă; funcția cosinus poate lua și valori negative pe acel interval. este strict descrescatoare pe
este strict descrescatoare pe ![Rendered by QuickLaTeX.com [0;\frac{\pi}{2}],](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-ec5c53089d9725efc2ccdd94869798ce_l3.png)
 deduc
deduc  , deci sup|f(x)|=M<1.
, deci sup|f(x)|=M<1.
Rezultatul de mai sus s-ar putea aplica doar dacă integrala ar avea și un n infață, iar intervalul de integrare ar fi [0;b], cu b<pi/2, ca atunci când fac schimbarea de variabilă să trec într-un interval de forma [a; 1], ca în teoria prezentată.
Observând că funcția
din
Atunci
Ultima expresie are limita 0 datorita lui M subunitar, ceeace rezolvă problema. Observi importanța premizei că 0<a<b<pi/2.
Da,m-au lasat neuronii!!! Am mai discutat cu dumneavoastra aceasta limita aici:

https://imgur.com/FIdMUkb
Numai ca acolo eu nu v-am spus nimic de modul in care am incercat sa o rezolv.
Multumesc mult.
In concluzie ,putem folosi cu incredere rezultatul expus de dumneavoastra?
Uitasem. Legat de observatie,aveti dreptate.Este o neatentie de-a mea. Se vede si din grafic ca acea functie ia valori si negative pe acel interval.
Vezi avantajul că te lasă neuronii? Fiecare problemă ți se pare … nouă și inedită.🙂
Iar întrebarea cu încrederea vrea să însemne: pune domne și o demonstrație, că altfel n-am încredere?
Nu am vrut sa spun ca nu am incredere in dumneavoastra ( mai ales ca va urmaresc de atata timp pe acest site si apreciez calitatea exceptionala a ideilor cu care veniti in rezolvarea unor probleme, de la care am invatat atatea lucruri noi ),dar stiti bine ca si la olimpiada orice rezultat folosit in solutionarea unei probleme necesita o mica demonstratie.Tot spuneati ca nu e nimeni interesat…asa ca ne-am bucura toti daca ar exista si o demonstratie
Multumim,domnule profesor ghioknt.
Eu am contat pe următoarea afirmație:![Rendered by QuickLaTeX.com a\in (-1;1),\;f:[a;1]\to \mathbb{R}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-bd604a94bc103eb80ee56d3393873a68_l3.png) este derivabilă și cu derivată continuă, atunci
este derivabilă și cu derivată continuă, atunci

Dacă
1) Dacă f este continuă, atunci

 .
. .
.
În cazul a>0,
În cazul a<0,
În ambele cazuri am folosit mărginirea unei funcții continue, iar expresiile finale au limita 0 pentru că a sau -a sunt pozitive subunitare.
2) Dacă, în plus, f este derivabilă și cu derivată continuă,
Evident, primul termen are limita f(1), iar al doilea, speculând ca mai sus mărginirea lui f’, are limita 0.
3) În concluzie,
Multumim,domnule profesor ghioknt.Un rezultat intr-adevar foarte util.Trebuie adaugat in caietul cu „retete” si scos de acolo la nevoie.