Buna ziua!
Se da multimea A= multimea tuturor numerelor de forma a+bxradical din 3,unde a si b apartin lui Z.
Se cere sa se arate ca multimea B=multimea tuturor elemente X apartinand lui A cu proprietataea ca [X]=0, are cel putin 2017 elemente!
Va multumesc frumos!
bxradical din 3 inseamna b inmultit cu radical din 3.


Primul pas este sa demonstrezi ca .
.
Apoi te gandesti cum poti sa construiesti 2017 numere din A a caror parte intreaga sa fie 0.
Mai degrabă, primul pas ar fi să arătăm că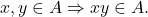
 și
și ![Rendered by QuickLaTeX.com [2-\sqrt{3}]=0...](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-8dfffe6ccdcf992ed91059f8a0cc5104_l3.png)
Apoi să observăm că
Eu propuneam sa construim sirul de numere![Rendered by QuickLaTeX.com x_n=-[n\cdot\sqrt{3}]+n\cdot\sqrt{3}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-dfa016cf316a5425b2dbc33ce0b52ab1_l3.png) .
.
Va multumesc frumos pentru raspunsuri!
Exercitiul este pentru clasa a 9-a.
Am tot incercat si am obtinut ca partea intreaga din bxradical din 3 =-a.
Dand apoi valori lui b in Z,sa zicem pt b=1,obtinem a=-1 care verifica,pt b=2 obtinem a=-3,si asa mai departe,obtin astfel o infinitate de solutii.
Ambele raspunsuri sunt pentru clasa a 9-a.
Nu se dau valori pentru rezolvarea problemei.
Atat solutia prezentata de mine cat si ideea sugerata de domnul profesor se bazeaza pe logica si demonstratie matematica.
PS: Solutia domnului profesor este interesanta si ar fi bine s-o duci si pe ea la capat.
Am dat valori doar pt a arata ca exista o infinitate de solutii,nu inteleg ce rost are acolo acel 2017.
Am tot incercat sa-i dau de cap,dar nu reusesc,sper sa reusesc cu indicatiile dvs.
Multumesc!
Adică Corect, excelentă idee. Dar greu de ghicit doar din indicație…
Corect, excelentă idee. Dar greu de ghicit doar din indicație… 🙂
Am ajuns,asa cum am scris mai sus la rezultatul urmator:
-a=partea intreaga din bxradical din 3.
Deci, a+bxradical din 3(care are partea intreaga=0)=bxradical din 3 -partea intreaga din bxradical din 3,deci exista o infinitate de numere de acest tip,oricare ar fi b in Z,nu?
E corect?
Fără supărare, scrieți în Latex, altfel pierd vremea să traduc ce ați postat, și chiar nu am timp de așa ceva. Dar, desigur, dacă nu vă interesează ce aș putea răspunde eu, nu folosiți Latex.
Din [a+b ]=a+[b
]=a+[b ]=0,rezulta ca [b
]=0,rezulta ca [b ]=-a,deci a+b
]=-a,deci a+b =b
=b
 ],numar care apartine multimii A,cu proprietatea ca partea intreaga din el este 0. Oricare ar fi b din Z,rezulta ca exista o infinitate de numere care satisfac cerinta.Nu inteleg ce rost are acel 2017 in exercitiu.
],numar care apartine multimii A,cu proprietatea ca partea intreaga din el este 0. Oricare ar fi b din Z,rezulta ca exista o infinitate de numere care satisfac cerinta.Nu inteleg ce rost are acel 2017 in exercitiu.
-[b
Este corecta rezolvarea?
Va multumesc frumos!
??
Vreau sa zic ca numerele de forma b -[b
-[b ] apartin lui A si au si proprietatea ca partea intreaga din ele este 0.
] apartin lui A si au si proprietatea ca partea intreaga din ele este 0.
E in regula?
Trebuie sa demonstrezi ca sunt unice. Altfel solutia nu e corecta. si
si ![Rendered by QuickLaTeX.com B_x=\begin{Bmatrix} y| y \in A_x,\;[y]=0 \end{Bmatrix}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-ac73f593502caa56273932e8662cd8f4_l3.png)
 este finita daca si numai daca x este numar rational.
este finita daca si numai daca x este numar rational.
Nu trebuie sa te incurci in cerintele problemei. Uneori ele sunt mai „slabe” doar pentru a face problema sa „sune” mai frumos.
Altfel, putem generaliza problema astfel:
Fie
Sa se demonstreze ca multimea
Am incercat toate pistele. ],este unic,nu?
],este unic,nu?
Daca b este unic,atunci si a=-[b
Dar b ia o infinitate de valori,atunci si a ia o infinitate de valori,nu?
Corect, insa trebuie sa demonstrezi ca si este unic.
este unic.
Uite, poti sa spui cine este Ax si cine este Bx pentru unul dintre cele mai simple cazuri, x=1?
Pentru fiecare b, exista un a unic astfel incat a=-[bx]. Si cu toate acestea B1 are …. elemente. Completeaza punctele de suspensie.
Unicitatea este simplu de demonstrat!
Puteti sa dati si dvs o rezolvare corecta a exercitiului?
Concluzia nu e directa. cu
cu  . In acel caz, desi exista o infinitate de b si o infintate de a, singurul numar care verifica identitatea [a+b*1]=0 este 0.
. In acel caz, desi exista o infinitate de b si o infintate de a, singurul numar care verifica identitatea [a+b*1]=0 este 0.
Inlocuieste
Vezi generalizarea data de mine mai sus.