Home/ Intrebari/Q 92441
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

jpg
Pe: 2017-11-30T11:40:06+02:00 In: In:

ecuatia cilindrului circumscris sferelor

Sa se det ecuatia cilindrului circumscris sferelor:
s1 : x ^ 2 + y ^ 2 + z ^ 2 = 1
s2 : (x-2) ^ 2 + (y+1) ^2 + (z-3) ^ 2 = 1
Încercarea mea:
https://ibb.co/kYiNpb
E corecta abordarea mea ?
Trebuie sa obtin 2 suprafețe?

Similare

5 raspunsuri

  1. gigelmarga
    profesor

    Ați putea avea măcar bunul simț să postați o poză care nu e rotită cu 90 de grade?

  2. jpg

    gigelmarga post_id=110045 time=1512072150 user_id=20599 wrote:
    Ați putea avea măcar bunul simț să postați o poză care nu e rotită cu 90 de grade?

    Da,ma scuzati !
    https://ibb.co/kfm4nw

    Attached files

  4. Integrator
    maestru (V)

    jpg post_id=110039 time=1512042006 user_id=22553 wrote:
    Sa se det ecuatia cilindrului circumscris sferelor:
    s_1 : x ^ 2 + y ^ 2 + z ^ 2 = 1
    s_2 : (x-2) ^ 2 + (y+1) ^2 + (z-3) ^ 2 = 1
    Încercarea mea:
    https://ibb.co/kYiNpb
    E corecta abordarea mea ?
    Trebuie sa obtin 2 suprafețe?


    Bună dimineața,

    Cunoscând care sunt valorile razelor celor două sfere putem stabili tipul cilindrului circumscris acestora.Ce poziție trebuie să aibă generatoarea cilindrului circumscris celor două sfere față de dreapta care unește centrele celor două sfere?Știind care este această poziție atunci putem determina ecuația cilindrului circumscris celor două sfere.
    ––––––––––––
    De ce credeți că ar trebui să obțineți două suprafețe?

    Toate cele bune,

    Integrator

  5. jpg

    Integrator post_id=110047 time=1512110463 user_id=14570 wrote:
    [quote=jpg post_id=110039 time=1512042006 user_id=22553]
    Sa se det ecuatia cilindrului circumscris sferelor:
    s_1 : x ^ 2 + y ^ 2 + z ^ 2 = 1
    s_2 : (x-2) ^ 2 + (y+1) ^2 + (z-3) ^ 2 = 1
    Încercarea mea:
    https://ibb.co/kYiNpb
    E corecta abordarea mea ?
    Trebuie sa obtin 2 suprafețe?


    Bună dimineața,

    Cunoscând care sunt valorile razelor celor două sfere putem stabili tipul cilindrului circumscris acestora.Ce poziție trebuie să aibă generatoarea cilindrului circumscris celor două sfere față de dreapta care unește centrele celor două sfere?Știind care este această poziție atunci putem determina ecuația cilindrului circumscris celor două sfere.
    ––––––––––––
    De ce credeți că ar trebui să obțineți două suprafețe?

    Toate cele bune,

    Integrator

    Cred ca obtin 2 suprafete deoarece relatiile cil pot fi inlocuite atar in euatia primei sfere ,cat si a celei de -a doua

  6. Integrator
    maestru (V)

    jpg post_id=110050 time=1512114055 user_id=22553 wrote:
    Cred ca obtin 2 suprafete deoarece relatiile cil pot fi inlocuite atar in euatia primei sfere ,cat si a celei de -a doua


    Bună dimineața,

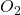    Deoarece este vorba despre cilindrul circumscris celor două sfere , atunci rezultă că generatoarele acelui cilindru sunt tangente la cele două sfere S_1 și S_2 și a căror raze sunt respectiv egale și anume R_1=R_2=1 , iar generatoarele cilindrului sunt paralele cu dreapta care unește centrele O_1 și respectiv O_2 ale celor două sfere , unde O_1 este chiar originea O a sistemul de axe ortogonale XOYZ.Cum găsim ecuația planului care trece prin originea sistemului de axe ortogonale XOYZ și care este perpendicular pe dreapta O_1O_2?
    –––––––-
    Spuneți , practic , cum am putea circumscrie doi cilindri diferiți celor două sfere.De ce doi cilindri și nu trei sau patru și etc.? 💡

    Numai bine,

    Integrator

Raspunde

Raspunde