Home/ Intrebari/Q 92160
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

liviu_paul98
Pe: 2017-04-19T14:42:03+03:00 In: In:

UTCN 899

Multimea valorilor lui y din R pentru care ecuatia \frac{[x]}{1+\{x\}} = y NU are solutii este ?

Raspunsul corect este [-\frac{1}{2}, \frac{1}{2}]

Similare

4 raspunsuri

  1. MaTe1997

    Se pleaca de la faptul ca 0\leq \{x\}<1 .In continuare construim fractia.Astfel ca Adunam un 1 si va rezulta 1\leq 1+\{x\}<2 .Ridicam la puterea -1,si se schimba inegalitatea.Rezulta:
    \frac{1}{2}<\frac{1}{ 1+\{x\}}\leq 1 .
    In continuarea avem 2 cazuri,cand x>0 si cand x<0.Mai intai inmultim inegalitatea in cazul in care x>0 ,astfel ca semnele nu se schimba ,de unde rezulta: \frac{[x]}{2}<y \leq[x] .Observam ca valoarea minima a [x] este 0 cand x pozitiv si apartine intre [0,1).Dar pentru aceste valori nu verifica inegalitatea .Deci se observa ca inegalitatea este adevarata si ca y are solutii in orice interval de forma (k/2,k] unde k numar intreg pozitiv nenul.(De ex pt x=1.2 se obtine 1/2<y<=1.)
    Luand analog celalalt caz cand x<0 se obtine [x] \leq y <\frac{[x]}{2} ,tinand seama de faptul ca x<0,se observa ca pentru orice x<0 inegalitatea este adevarata si ca y are solutii in orice interval de forma [k,k/2) unde k numar intreg negativ nenul.(De ex pt x=-0.7 se obtine -1<=y<-1/2.)
    Rezulta ca egalitatea din enuntul tau nu are solutii in intervalul [-1/2;1/2].

  2. ghioknt
    profesor

    Dar pentru y=0? Nu cumva orice x din [0; 1) este solutie?

  4. Integrator
    maestru (V)

    MaTe1997 wrote: Se pleaca de la faptul ca 0\leq \{x\}<1 .In continuare construim fractia.Astfel ca Adunam un 1 si va rezulta 1\leq 1+\{x\}<2 .Ridicam la puterea -1,si se schimba inegalitatea.Rezulta:
    \frac{1}{2}<\frac{1}{ 1+\{x\}}\leq 1 .
    In continuarea avem 2 cazuri,cand x>0 si cand x<0.Mai intai inmultim inegalitatea in cazul in care x>0 ,astfel ca semnele nu se schimba ,de unde rezulta: \frac{[x]}{2}<y \leq[x] .Observam ca valoarea minima a [x] este 0 cand x pozitiv si apartine intre [0,1).Dar pentru aceste valori nu verifica inegalitatea .Deci se observa ca inegalitatea este adevarata si ca y are solutii in orice interval de forma (k/2,k] unde k numar intreg pozitiv nenul.(De ex pt x=1.2 se obtine 1/2<y<=1.)
    Luand analog celalalt caz cand x<0 se obtine [x] \leq y <\frac{[x]}{2} ,tinand seama de faptul ca x<0,se observa ca pentru orice x<0 inegalitatea este adevarata si ca y are solutii in orice interval de forma [k,k/2) unde k numar intreg negativ nenul.(De ex pt x=-0.7 se obtine -1<=y<-1/2.)
    Rezulta ca egalitatea din enuntul tau nu are solutii in intervalul [-1/2;1/2].

    Ce valoare are x pentru y=0?

  5. MaTe1997

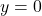    Corect,m-am gandit la cazul cand y=0 ,dar am omis sa-l trec,oricum nu ne intereseaza pt ca avem nevoie doar de acei y pt care nu e solutie.Multumesc pentru observatia facuta!Toate cele bune!

Raspunde

Raspunde