![]()
n este din N*, fixat (am incercat sa scriu Latex, dar nu functioneaza)
1) Aflati perioada principala a lui ![]() .
.
Am folosit formula ![]() ,
, ![]() avand perioada principala
avand perioada principala ![]() am afirmat ca intreaga functie are aceeasi perioada principala. Este corect ?
am afirmat ca intreaga functie are aceeasi perioada principala. Este corect ?
2) Functia ![]() are o primitiva periodica daca si numai daca c are valoarea ? (Raspunsul este
are o primitiva periodica daca si numai daca c are valoarea ? (Raspunsul este ![]() )
)


1) Răspunsul mi se pare corect.
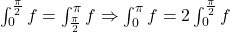 cu schimbarea t=pi-x.
cu schimbarea t=pi-x.
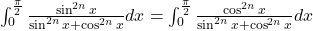 cu t=(pi/2)-x. Atunci
cu t=(pi/2)-x. Atunci
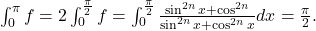
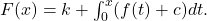
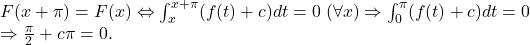
2) Dacă primitiva F are perioada T, atunci şi f o admite; cum cea mai mică perioadă a lui f este pi, atunci, dacă F este periodică,
pi este cea mai mică perioadă posibilă şi pentru ea.
Orice primitivă a lui f+c este de forma
Obs. Chiar dacă nu e clar că pi este perioada principală a lui F, aceasta trebuie totuşi să fie de forma mpi. Acest m apare
şi în ultima relaţie, dar se simplifică.
Stiu ca e stupida intrebarea dar… de ce primitiva functiei are forma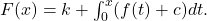 ? De unde acel k si de ce integrala de la 0 la x ? Multumesc frumos pentru rezolvare !
? De unde acel k si de ce integrala de la 0 la x ? Multumesc frumos pentru rezolvare !
Vei învăta în curând o teoremă foarte importantă: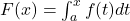 este
este
dacă f este o functie continuă pe un interval, atunci, pentru orice a din interval, functia
o primitivă a lui f (si anume, primitiva care se anulează în a).
Stii deja că oricare 2 primitive diferă printr-o constantă, de aici misteriosul k.