Un mobil porneste cu viteza initiala v0=15m/s. Dupa un timp t’, mobilul trece prin punctul de coordonata x’=10m cu o viteza v’=-10m/s.Sa se calculeze>
a)acceleratia
b)timpul t’
c)distanta parcursa in acest timp
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Sper ca stii legile de miscare (parca se mai spun si ale lui Galilei).
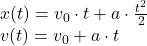
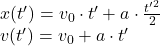
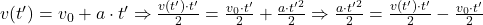
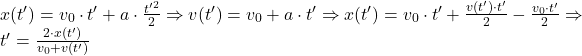
Avem
Pentru cazul nostru:
Inlocuim in prima ecuatie a legii de miscare (cea referitoare la distanta).
Um, stiu ca iti cer prea mult, dar ai putea sa imi explici, te rog, cum sa gandesc o problema de genul?Adica cum aflu acceleratia,timpul t’, distanta, viteza in modul?Dau test si nu am inteles absolut nimic, stiu doar formulele generale pentru ca le am invatat mot a mot.
Daca nu poti, nu e nicio problema, iti multumesc frumos pentru rezolvarea data!
1. E foarte important sa intelegi de ce rezolvarea e corecta.
2. Aceasta problema are nevoie de un mic artificiu pentru rezolvare.
Putem afla o necunoscuta dintr-o ecuatie, doar daca restul elementelor sunt stiute. Atunci cand avem un sistem de ecuatii, putem incerca sa eliminam din necunoscute. Exact acest procedeu am folosit eu in rezolvarea problemei.
In ambele ecuatii avem 2 necunoscute, timpul respectiv acceleratia. Ti-am dat o metoda cum poti elimina acceleratia si ajungi la o singura ecuatie cu o singura necunoscuta.
Poti sa exprimi acum acceleratia in functie de datele cunoscute in problema?
Poti posta o altfel de problema pentru a intelege mai bine ce nelamuriri ai.
Ar fi foarte bine daca nu ai invata pe de rost legile de miscare. De exemplu, a doua ecuatie ar trebui sa fie usor de inteles.
Prima ecuatie o vei putea intelege pe deplin in clasa a 12-a, dupa ce inveti integralele la analiza matematica.
Multumesc mult!Cred ca am inteles cum trebuie rezolvata!Voi incerca sa inteleg ecuatiile miscarii!Daca voi mai avea nelamuriri, sper sa dau peste oameni ca tine, sau chiar peste tine!😀
Nu-nteleg!Viteza poate fi negativă?
Si eu am fost uimita, dar asa a dictat profesorul🙁
Cred ca din cauza ca viteza este negativa, de asta trebuie sa dea si acceleratia negativa la subpunctul a).
Ganditi-va la aruncarea unui obiect pe verticala. Obiectul va avea o viteza v0>0, dar a=-g. Considerand axa Ox in sus, atunci la intoarcere viteza va fi negativa.
Problemele oricum sunt pur teoretice, dar hai sa presupunem ca in cazul problemei date rotile se contrar sensului de mers. Atunci acceleratia este negativa, iar la un moment dat masina va merge inapoi, ceea ce inseamna viteza negativa in conformitate cu axa aleasa.
L.E.: Am reeditat pentru a face enuntul ceva mai clar.
Multumim pentru raspuns!
Nu-nteleg…
Problema nu vorbeste despre aruncarea unui obiect pe verticală…Vectorul viteză
Ati intrebat in ce caz viteza ar putea fi negativa. Am dat intai cel mai simplu caz in care se intampla asa ceva. Considerati ca aruncam o masina de jucarie. Daca punem o singura axa, atunci putem ajunge usor la datele problemei.
Iar problema chiar asta sugereaza. Avem un mobil care pleaca cu o viteza v0, dar cu acceleratie negativa. O analogie (fara a avea pretentia de miscare uniform accelerata) ar fi cu bila de biliard/snooker, care este lovita cu efect de intoarcere. t=0 este momentul in care bila este lovita, datorita conservarii impulsului va avea o viteza initiala, dar datorita efectului de intoarcere, acceleratia va fi negativa, iar bila se va opri si se va intoarce.
Intr-adevar, la un moment dat viteza va fi 0. Dar asta nu este relevant. Iar cand discuta de viteza, se discuta de viteza pe axa problemei, cu alte cuvinte, viteza ramane un vector si nu un scalar.
Avand in vedere ca viteza initiala este pozitiva, iar cea din punctul x’ este negativa, deducem usor de rapid ca e foarte de viteza pe care o are mobilul atunci cand se intoarce deja.
Nu-nteleg!
1) Cum scrieti Dvs. ecuatia vitezei în miscarea uniform încetinită?
2) Nu am înteles ce vreti să spuneti în fraza „Avand in vedere ca viteza initiala este pozitiva, iar cea din punctul x’ este negativa, deducem usor de rapid ca e foarte de viteza pe care o are mobilul atunci cand se intoarce deja.”.
1. Indiferent daca acceleratia este pozitiva sau negativa, tot timpul voi scrie:
x=x0+Vo*t+a*(t^2)/2. Iar pentru ca dumneavoastra stiti de fapt ca distanta este variatia vitezei in functie de timp, adica integrala vitezei in functie de timp, sunt sigur ca intelegeti complet formula pentru o miscare uniform accelerata. Sau uniform incetinita, asa cum o formulati.
2.🙂 . Este evident ca nimeni nu poate sa priceapa ce-am scris acolo. Voi incerca sa reformulez ceva mai tarziu.
LE: Am scris un „foarte” in loc de „vorba”. Acum are sens, cel putin pentru mine, si trebuie citit ca mai jos. Este posibil sa fie persoane carora le este greu sa descifreze ce am incercat sa transmit. Imi asum eventuale critici pentru modul in care am formulat.
„Avand in vedere ca viteza initiala este pozitiva, iar cea din punctul x’ este negativa, deducem usor de rapid ca e vorba de viteza pe care o are mobilul atunci cand se intoarce deja.”
––––––––––––––––-
As vrea insa sa plecam de la niste premise.
1. Nu trebuie sa acordam prea mare atentie datelor problemei. Este o problema pur teoretica.
2. Viteza si acceleratia sunt considerate tot timpul vectori, intr-un sistem unidimensional. De aici deducem ca valorile negative au sens.
3. Mobilul pleaca cu viteza v0, dar cu acceleratie negativa, ajunge in punctul de maxima departare, dupa care se intoarce.
Putem gasi tot felul de scenarii in care acest scenariu sa aiba loc.8) ne apropiem destul de mult de datele problemei.
Uitati un exemplu.
Avem o minge la baza unui plan inclinat. Daca sutez in minge, in susul planului inclinat suntem exact in situatia in care mobilul/mingea are o viteza initiala si acceleratie negativa. Pentru un unghi alfa=arcsin(6.25/9.
PS: Sper ca n-am mai scris ceva care n-are nici un sens.
1. Relatia
Întrebări:
Nu-nteleg afirmatia „distanta este variatia vitezei in functie de timp”?!
Care este ecuatia vitezei în miscarea uniform încetinită si în cea uniform accelerată si cum poate rezulta din aceste ecuatii că viteza ar putea fi negativă?
2. Fără supărare dar,nu-nteleg „Avand in vedere ca viteza initiala este pozitiva, iar cea din punctul x’ este negativa, deducem usor de rapid ca e vorba de viteza pe care o are mobilul atunci cand se intoarce deja.”.Viteza ca scalar nu pote fi niciodată negativă.
––––––––––––––––––-
1. Este gresit să spunem
2. De-acord, ca vectori ,dar ca scalar niciodată viteza nu poate fi negativă.
Cum se întoarce mobilul dacă nu atinge mai întâi valoarea zero a vitezei?!
Să lăsăm alte scenarii de genul „aruncării pe verticală” sau de genul „aruncării pe un plan înclinat”…Vă rog frumos , rezolvati problema asa cum a fost enuntată de autor.
Multumesc mult!
1. In ecuatia miscarii uniform accelerate, x este vectorul pozitie si nu distanta de la origine. Poate de aici vine confuzia dumneavoastra.

Cititi ce reprezinta fiecare variabila in parte.
2. Nu este nevoie sa definim miscare uniform incetinita. Este suficienta formula miscarii uniform accelerate in care vectorul acceleratia este opus sensului axei. Adica este negativa.
La fel cum nu este nevoie sa definim miscare uniform rectilinie pozitiva si uniform rectilinie negativa, la stanga, la dreapta, in sus sau in jos.
3. Daca v=v0+at si a este negativ, nu credeti ca v ar putea fi negativ?
De ce este gresit sa spunem ca viteza ar fi negativa?
4. Este evident ca viteza va fi 0 la un moment dat (adica vector nul). A zis cineva altfel?! Mobilul va trece de 2 ori prin punctul x’. O data la dus, cand vectorul viteza este in sensul axei ales si inca o data la intoarcere, cand vectorul viteza este opus sensului axei.
5. Problema a fost rezolvata. Va place sau nu. V-am propus un plan inclinat pentru a intelege de ce acceleratia poate fi negativa si viteza initiala pozitiva.
Bonus:
Va rog sa scrieti ecuatiile de miscare ale unui corp aruncat oblic la un unghi alfa (0<alfa<90).
Veti avea posibilitatea sa spargeti vectorul pozitie in 2 vectori. Sa spargeti vectorul viteza in 2 vectori. Sa analizati o miscare uniform accelerata si una uniform rectilinie.
Şi discuţiile despre fizică pot fi pasionante, aşa că mă bag şi eu.
Numerele negative au fost o mare invenţie în matematică, iar fizica a beneficiat şi totodată a provocat multe dintre aceste invenţii.
Cea mai adecvată scriere a ecuaţiilor mişcării, fie ea şi cea mai simplă – mişcarea rectilinie, este scrierea vectorială.
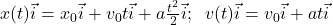
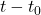 . Eu zic că şi variabila t poate fi negativă dacă vrem să aflăm elemente din trecut ale mişcării,
. Eu zic că şi variabila t poate fi negativă dacă vrem să aflăm elemente din trecut ale mişcării, 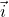 este versorul cu care este dotată orice axă, iar
este versorul cu care este dotată orice axă, iar 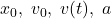 sunt
sunt 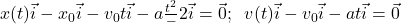 apoi
apoi
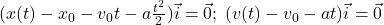
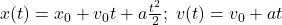
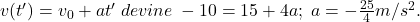
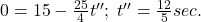
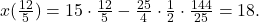
sunt ecuaţiile mişcării uniform accelerate în care datele iniţiale sunt cele de la momentul 0, altfel ecuaţiile ar fi mai complicate,
în loc de t, ar trebui scris
adică de dinaitea momentului iniţial.
În ecuaţiile de mai sus
nişte scalari care au dreptul şi trebuie să fie negativi dacă vectorii respectivi au sensul contrar versorului axei.
Dacă scriem
este clar că parantezeke trebuie să aibă valoarea 0, deci se obţine
relaţii în care scalarii au aceleaşi semne + sau – ca în relaţia vectorială. A spune că la momentul final t’=4sec viteza este
-10 m/sec nu este o greşeală, ci o simplă convenţie facilitată de invenţia numită numere negative, menită să arate că,
în acel moment, vectorul viteză are sens contrar sensului pozitiv al axei, dat prin versorul său.
Să finalizăm problema. Din ultima relaţie scrisă de A_Cristian aflăm t’=4s.
Dacă notăm t” momentul în care viteza devine 0, din ecuaţia vitezei:
Spaţiul parcurs până la oprire:
Dacă ar mai fi mers 10m ar fi ajuns în punctul de plecare, deci în cele 4 secunde a parcurs 18+(18-10)=26m.
Viteza în modul medie este 26/4= 6,5 m/s.
Aceleaşi ecuaţii, numite ale mişcării uniform accelerate, descriu mişcarea şi în cazul în care zicem că mişcarea este încetinită.
Zicem că mişcarea este uniform încetinită, atunci când, pe un anumit interval de timp, viteza şi acceleraţia au semne contrare
şi zicem că este propriu-zis accelerată, atunci când cele doua au acelaşi semn, deci nu când acceleraţia este negativă sau pozitivă.
În problema noastră acceleraţia este constantă si exprimată printr-un număr negativ. În primele 12/5=2,4 sec mişcarea este
‘încetinită” petru că viteza se exprimă printr-o funcţie cu valori pozitive, v(t)=15-(25t)/4. După acest moment viteza şi acceleraţia
sunt ambele negative, iar mişcarea este propriu-zis accelerată. Mobilul se îndreaptă spre -oo cu o viteză în modul din ce în ce mai
mare. Pur şi simplu putem să zicem că forţa care stă în spatele acestei acceleraţii „negative” nu se mai opune mişcării, ci o provoacă.
Îmi cer scuze lui A_Cristian pentru că m-am băgat ca musca-n lapte peste rezolvarea şi argumentaţia lui, pe care le găsesc
fără reproş, dar provocarea pentru mine a fost ca fie Delia, fie Integrator să fie de acord cu unele din zisele mele.
Imi pare bine ca aceasta problema a starnit o adevarata discutie aici!
As dori sa intreb, daca se poate,voi cum ati „povesti” cele trei subpuncte pe intelesul elevilor mai slabi, astfel incat sa dea reyultatele corecte?
Numerele negative dau multe bătăi de cap mai ales în cazul radicalilor de indice par , dar problema de fizică asa cum a fost enuntată initial si chiar după ce a fost enuntată altfel mi se pare a avea lipsă un amănunt important si anume că valoarea acceleratiei în modul este aceiasi pe toată distanta parcursă pe toată peroada de timp
Nu am timp acum , dar ,pentru cine doreste, eu pot scrie ecuatiile miscării acelui mobil pe distanta
––––––––––––––––––––––
După părerea mea enuntul problemei ar trebui să fie următorul:
Un mobil porneste uniform variat si rectiliniu pe axa din originea sa si în sensul pozitiv al acesteia, cu viteza initială
din originea sa si în sensul pozitiv al acesteia, cu viteza initială 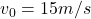 . După un timp
. După un timp 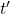 , mobilul trece prin punctul de coordonată
, mobilul trece prin punctul de coordonată 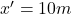 cu o viteza
cu o viteza 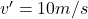 iar vectorul viteză la acest moment are sensul opus sensului pozitiv al axei
iar vectorul viteză la acest moment are sensul opus sensului pozitiv al axei  .Stiind că pe tot parcursul drumului până în punctul de coordonată
.Stiind că pe tot parcursul drumului până în punctul de coordonată  valoarea scalară în modul a acceleratiei este aceiasi atunci să se calculeze:
valoarea scalară în modul a acceleratiei este aceiasi atunci să se calculeze: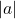 .
.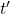 .
.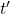 .
.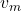 cu care mobilul a parcurs distanta în timpul
cu care mobilul a parcurs distanta în timpul 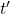 .
.
a) acceleratia în modul
b) timpul
c) distanta parcursă în timpul
d) viteza medie
Exemplu dat de Dvs. în care ati omis a da o dată foarte importantă (Care este acea dată omisă de Dvs.?) nu se aseamănă cu problema enuntată de autor în care s-a omis să se dea referiri cu privire la valoarea acceleratiei pe traseu si în acest sens propun un studiu de cazuri privind aruncarea corpurilor pe verticală.
Dacă este vorba despre Terra , atunci la aruncarea unui obiect pe verticală există două cazuri:
1) aruncarea de la suprafata Terrei a obiectului.
2) aruncarea către suprafata Terrei a obiectului de la înăltimea
Care sunt ecuatiile scalare ale miscării obiectului în cele două cazuri?
Ce rost are aceasta discutie daca nu vreti sa intelegeti ca ecuatiile de miscare sunt pur vectoriale? V-am dat referinte, dar ati trecut peste ele ca si cum n-ar exista. Nu conteaza ce-ati invatat sau credeti ca ati invatat la scoala.
Este evident ca ecuatiile se vor scrie diferit in functie de orientarea axei alese sau a originii. Sensul si originea axei se aleg in mod convenabil.
Ecuatiile vectoriale descriu foarte bine fenomenul si nu este nevoie de altceva.
Nu ma intereseaza cazuri particulare si nici sa sparg o ecuatie simpla in 2 ecuatii pentru primul caz.
Are rost discutia pentru că eu nu-nteleg cum poate fi negativă valoarea scalară a unei viteze….
Haideti să studiem atunci , ecuatiile Dvs. vectoriale în cazurile 1) si 2) propuse de mine pentru aruncarea pe verticală a unui obiect.Scrieti ,vă rog frumos, acele ecuatii vectoriale conform dorintei Dvs. dar în cazurile propuse de mine.
Multumesc!
Cumva ar putea fi legat de faptul ca „https://en.wikipedia.org/wiki/Scalar_%28physics%29” desemneaza ceva ce se poate reprezenta/masura printr-un {numar real} si nu de un {numar real pozitiv}?! Temperatura este un scalar, sarcina electrica este un scalar, potentialul electric este un scalar etc.