Buna,
Sa se determine numerele reale a si b astfel incat {x∈R | x^2+2ax+b=0}\{x∈R | x^2+2bx+a=0}=∅.
Va rog daca stie cineva cum se face acest exercitiu.
Am incercat sa pun toate conditiile care ar merge, ba primul determinant sa fie negativ, iar al doilea pozitiv, sau egal cu zero sau negativ. Ba ambii determinanti sa fie zero si radacinile diferite. Nu ajung la nimic frumos, ajung la multe litere pe care nu stiu cum sa le mai grupez. Am aflat ca s-ar face usor cu tabelul de variatie al functiei de gradul 2, dar inca nu am ajuns la acea lectie la scoala.
Va multumesc


Problema spune ca daca exista un x real care satisface x^2+2ax+b=0, atunci el trebuie neaparat sa satisfaca si cealalta ecuatie, adica x^2+2bx+a=0.
Fie A={x∈R | x^2+2ax+b=0} si B={x∈R | x^2+2bx+a=0}.
Mergem pe cazul cand A nu este vida. Fie t∈A. Atunci avem:
t^2+2at+b=0
t^2+2bt+a=0.
Scadem cele 2 relatii si obtinem ca 2t(a-b)=a-b.
Daca a=b, atunci A=B si nu trebuie sa mai studiem nimic. (Te rog sa spui exact de ce nu e nevoie).
Daca a<>b, atunci t=1/2. Acum putem calcula usor care sunt elementele multimii A si care sunt elementele multimii B. (Te rog sa spui exact ce elemente are A si ce elemente are B).
Spor si te astept cu solutia sau intrebari.
Multumesc mult de tot pt raspuns.
Deci cand a=b nu mai studiem nimic pt ca A fiind egala cu B inseamna ca diferenta e multimea vida, A nemaiavand si alte elemente diferite de cele ale lui B. Chestia e ca la final precizeaza ca daca a=b, a apartine intervalului (-infinit, 0] U [1, infinit] si nu stiu cum sa demonstrez asta.
Iar daca a<>b, atunci o sa avem a+b+1/4=0, a,b apartin R.
Si cand A e vida? scriem direct D<0, adica a^2<b si atat?
Va doresc multa sanatate !
Daca ai un raspuns diferit, inseamna ca n-ai postat complet problema. Este posibil sa fie niste conditii suplimentare, de exemplu ca A si/sau B sa nu fie vide. Asta ar duce la rezultatul afisat la finalul cartii/culegerii.
N-ai terminat cazul a<>b. In cazul asta stii deja o radacina si o poti afla pe cealalta foarte simplu. Singura chestie pe care trebuie s-o mai faci este sa verifici ca a doua radacina a ecuatie x^2+2ax-a-1/4=0 se afla si ea in B.
Vezi daca mai trebuie sa studiezi cazul cand A este vida.
Incerc aici sa pun pozele cu enuntul si raspunsul de la final.
Este exercitiul 1.
Imi pare rau de calitatea atat de proasta a pozelor.
„https://postimg.org/image/baejg3ab7/”>https://postimg.org/image/baejg3ab7
Daca a=b, atunci pe (0,1) avem ca a^2<a=b. De aici si al doilea raspuns. Insa eu am obtinut alte rezultate in ceea ce priveste a<>b. Tocmai de aceea te-am rugat sa identifici pe A si B in acel caz.
Asa ca te rog a 3-a oara sa spui cat sunt A si B atunci cand a+b+1/4=0.
1)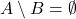 pentru
pentru 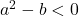 ceea ce este evident deoarece elementele multimii
ceea ce este evident deoarece elementele multimii  sunt numere complexe.
sunt numere complexe.
2)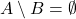 pentru
pentru  cu
cu 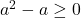 adică pentru
adică pentru ![Rendered by QuickLaTeX.com a\in (-\infty,0] \cup [1,+\infty)](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-055fa118fd7aa29316276d7a222a6e9b_l3.png) deoarece cele două multimi au aceleasi elemente.
deoarece cele două multimi au aceleasi elemente.
3)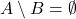 pentru
pentru 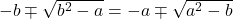 sau pentru
sau pentru 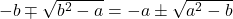 sau pentru
sau pentru 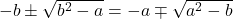 adică pentru
adică pentru 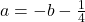 , deoarece cele două multimi au aceleasi elemente.Relatia
, deoarece cele două multimi au aceleasi elemente.Relatia 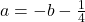 se obtine din rezolvarea ecuatiei de gradul III cu necunoscuta
se obtine din rezolvarea ecuatiei de gradul III cu necunoscuta  în functie ,de exemplu în acest caz, de parametrul
în functie ,de exemplu în acest caz, de parametrul  stiind că
stiind că 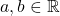 .
.
1. Aveti un fetis cu numerele complexe. Pentru un elev de clasa a 9-a ele nu exista!!
2. Am intrebat deja de 3 ori care sunt multimile A si B in cazul in care a+b+1/4=0. Si din pacate, in loc sa-i aratati asta, ati trecut iarasi la o alta extrema si anume ecuatii de grad 3, in conditiile in care eleva abia invata ecuatia de grad 2.
Avem:
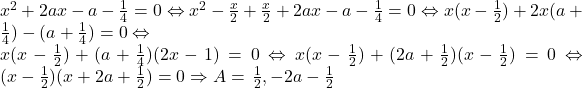
Cred ca este absolut evident ca:
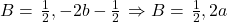
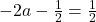 adica x=1/2 este radacina dubla.
adica x=1/2 este radacina dubla.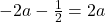 si ajungem ca a=b (ceea ce iarasi ne asteptam la un astfel de caz.
si ajungem ca a=b (ceea ce iarasi ne asteptam la un astfel de caz.
Mai departe avem de studiat exact 2 cazuri:
1.
2.
1. Tocmai pentru că numerele complexe nu „există” la clasaIX-a , atunci cu atât mai mult diferenta dintre A si B este multimea vidă…Pentru că acel discriminat este mai mic ca zero.
2. Care sunt multimile A si B în cazul
1. Exact asta trebuia sa scrieti. Discriminantul este 0, deci multimea A este vida, de unde rezulta ca diferenta este multima vida.
2. Daca va uitati atent la postul meu, veti descoperi care sunt multimile A si B. Sunt scrise cu litere mari si acolade. Mai mult, am scris si care este rezolvarea. Daca vi se pare ca ceva este neclar, va rog sa citati solutia si sa spuneti ce anume nu este clar explicat.
Daca avem o ecuatie de grad 2 si stim o radacina, atunci automat vom sti si a doua radacina. Chiar si acest lucru l-am exemplificat in postul meu.
Fără supărare,dar nu-nteleg…
1. Discriminantul
2. Ca să ajungeti să găsiti multimile
Imi permit să fac unele comentarii asupra acestei probleme.
1. Nu mi se pare normal să pretind să se determine anumite obiecte atunci când mulţimea soluţiilor este infinită.
2. Răspunsul meu la problema astfel formulată este: mulţimea A\B poate fi mulţimea vidă pentru orice valoare reală a parametrului a,
cât şi pentru orice valoare reală a parametrului b.
3. In realitate, obiectele care trebuie aflate aici nu sunt numerele reale a şi b, ci perechile de numere reale (a,b).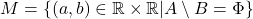 .
.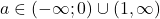 . Răspuns:
. Răspuns:
![Rendered by QuickLaTeX.com M=\left \{ (a,b)\in \mathbb{R}\times \mathbb{R}|b>a^2 \right \}\cup \left \{ (a,b)\in \mathbb{R}\times \mathbb{R}|b=a\;si\;a\in (-\infty ;0)\cup (1,\infty ) \right \}\cup \left \{ (0,0),\;(1,1),(-\frac{1}{2},\frac{1}{4}) \right \}=\\=\left \{ (a,b)\in \mathbb{R}\times \mathbb{R}|b>a^2 \right \}\cup \left \{ (a,b)\in \mathbb{R}\times \mathbb{R}|b=a\;si\;a\in (-\infty ;0]\cup [1,\infty ) \right \}\cup \left \{ (-\frac{1}{2},\frac{1}{4}) \right \}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-965ba464ce6dd9ea1bda9e448aca54f6_l3.png) .
.
Dacă este ceva de determinat, aceea este mulţimea
A (deci şi A\B) este mulţimea vidă pentru b>a^2.
A are un singur element, pe -a, pentru b=a^2; acesta trebuie să fie şi în B, adică să verifice şi a doua ecuaţie: a^2-2a^3+a=0,
cu soluţiile 0, 1, -1/2, iar pentru b valorile corespunzătoare sunt 0, 1, 1/4.
A are 2 elemente pentru b<a^2, iar atunci cele două ecuaţii trebuie să aibă aceleaşi rădăcini. Rămânem cu ansamblul de
condiţii b=a şi a<a^2, adică
4. De ce discutăm despre a+b+1/4=0? Pentru că apare la răspuns? Atunci singurul subiect de conversaţie ar putea fi:
care este problema pentru care perechile de numere reale care verifică relaţia de mai sus sunt soluţii.
1. Nu cred ca am zis undeva ca ar fi nevoie de acea conditie. Singura remarca la acest caz a fost mentionarea numerelor complexe pe care o consider inutila.
2. Ma citez:
De aici rezulta o conditie necesara, dar nu suficienta, si anume ca t=1/2.
Inlocuind pe t in ecuatiile initiale vom obtine:
a) (1/2)^2+2*(1/2)*a+b=0 adica a+b+1/4=0
b) (1/2)^2+2*(1/2)*b+a=0 adica a+b+1/4=0
Am mentionat doar acest caz pentru ca A= multime vida este un caz banal.
@ghioknt.
O problema poate avea mai multe rezolvari. a+b+1/4=0 apare strict din rezolvare pe care am incercat s-o schitez.
1. Nu cred ca am zis undeva ca ar fi nevoie de acea conditie. Singura remarca la acest caz a fost mentionarea numerelor complexe pe care o consider inutila.
2. Ma citez:
De aici rezulta o conditie necesara, dar nu suficienta, si anume ca t=1/2.
Inlocuind pe t in ecuatiile initiale vom obtine:
a) (1/2)^2+2*(1/2)*a+b=0 adica a+b+1/4=0
b) (1/2)^2+2*(1/2)*b+a=0 adica a+b+1/4=0
Am mentionat doar acest caz pentru ca A= multime vida este un caz banal.
@ghioknt.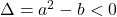 este un caz pentru ca să avem
este un caz pentru ca să avem 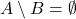 , iar discriminantul egal zero nu spune nimic dacă nu punem si conditia
, iar discriminantul egal zero nu spune nimic dacă nu punem si conditia  .”
.”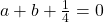 care rezultă din faptul că
care rezultă din faptul că  …nu era necesar să puneti
…nu era necesar să puneti  în loc de
în loc de  …
…
O problema poate avea mai multe rezolvari. a+b+1/4=0 apare strict din rezolvare pe care am incercat s-o schitez.
1. Repet:”Discriminantul
2. Am înteles , si rezolvarea Dvs. este elegantă pentru conditia
Multumesc mult pentru această rezolvare simplă si elegantă.
Da, m-am lămurit. Condiţia a+b+1/4=0 provine de la răspunsuri. Acolo scrie clar că numerele reale a şi b care verifică asta
sunt soluţii ale problemei. Cum ar fi bunăoară a=-1/4 şi b=0. Aşa să fie? Rezolvând prima ecuaţie obţinem A={1/2; 0}, iar
rezolvând-o pe a doua obţinem B={-1/2; 1/2}, deci A\B={0} care nu înseamnă mulţimea vidă. Singurele soluţii care verifică
această relaţie îmi par a fi (-1/2,1/4), (-/1/8,-1/8). Dar ele sunt deja incluse în mulţimea soluţiilor fără ajutorul ei.
Tot de la răspunsuri provine şi nefericita notaţie A, B pentru cele 2 mulţimi, notaţie pe care am preluat-o cu toţii fără pic de simţ critic.
În realitate, în această problemă nu apar 2 mulţimi, ci 2 familii de mulţimi, iar notaţiile potrivite ar fi A(a,b), B(a,b), mai ales pentru
a atrage atenţia unor elevi de clasa a 9-a asupra faptului că „conţinuturile” celor 2 mulţimi depind de o pereche de numere reale.
@ghioknt
1. a+b+1/4=0 apare in solutia de la spatele culegerii, dar aparitia ei acolo nu are legatura cu rezolvarea propusa de mine. Este o ecuatie dedusa. Va rog sa revedeti posturile mele.
2. Eu cred ca am spus clar ca pt a+b+1/4=0 avem exact 2 solutii care satisfac conditia initiala, din care o solutie este inclusa in cazul a=b. In rest, este evident ca A\B nu va fi vida pentru perechile (a, -a-1/4).
3. Nu este prima data cand vad solutii gresite. Am vazut rezolvari gresite in culegeri semnate de profesori destul de importanti* in matematica.
importanti = propunatori si rezolvitori de probleme. nu ma refer la cercetare.
@Integrator
Am spus ca nu are sens studiul cazului banal b>a^2. Toate perechile de numere care satisfac aceasta relatie satisfac si cerinta problemei.
Pentru cazul a^2=b nu e nevoie de studiu separat pentru ca ne aflam deja in cazul in care A are cel putin un element. Iar acest caz l-am analizat complet.
LE: Cred ca ar fi interesant pentru elevi, in cazul in care mai urmareste vreunul acest topic, sa dam si o interpretare geometrica a solutiei.
O interpretare geometrică a soluţiilor este aproape obligatorie. Punctele P(a,b) corespunzătoare soluţiilor problemei sunt:
regiunea din plan situată „deasupra” parabolei y=x^2, care este denumită şi interiorul parabolei (conţine focarul);
punctele dreptei y=x (prima bisectoare) dintre care cele coresponzătoare intervalului 0<x< 1 sunt incluse în interiorul parabolei,
aşa că mai rămân semidreptele ce corespund unui x din intervalele (-oo; 0], [1; oo);
punctul A(-1/2,1/4) situat pe parabolă.
Apreciez enorm toate raspunsurile.
Va multumesc mult tuturor