Fie f:R->R continua si F:R->R,F(x)=integrala de la 0 la x din f(t)dt,F(1)=1.Sa se arate ca exista a1,a2 apartine lui R astfel incat f(a1)*f(a2)=1.
Multumesc frumos!
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Fie f:R->R continua si F:R->R,F(x)=integrala de la 0 la x din f(t)dt,F(1)=1.Sa se arate ca exista a1,a2 apartine lui R astfel incat f(a1)*f(a2)=1.
Multumesc frumos!
Despre F putem spune şi că F(0)=1. Aşadar
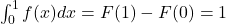(1)
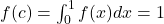(teoremă de medie).![f(x)\leq 1\;pe\;[0;1]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-9226354d123b7f49c60665c697705257_l3.png "Rendered by QuickLaTeX.com")
ar rezulta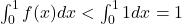 
,
În plus, există c în (0; 1) a. î.
Dacă f este constantă pe [0; 1], sau dacă există 2 puncte în care f ia valoarea 1, atunci concluzia este adevărată.
Să analizăm situaţia în care f(c)=1 într-un singur c. Afirm că dacă există x_1 în care 0<f(x_1)<1, atunci există şi x_2, ambele în [0; 1],
în care f(x_2)>1. Într-adevăr, din
ceeace contrazice (1). (Inegalitatea dintre integrale este strictă pentru că şi inegalitatea dintre funcţiile continue f şi 1 este
strictă măcar într-un punct.)
Presupunem că f(x_1)*f(x_2)>1. Sunt evidente inegalităţile f(x_1)<1<1/f(x_1)<f(x_2), şi din P. D. deducem că există
a_2 între x_1 şi x_2 în care f(a_2)=1/f(x_1). Luăm a_1=x_1: f(a_1)*f(a_2) =f(x_1)*(1/f(x_1))=1.
Dacă f(x_1)*f(x_2)<1: f(x_1)<1/f(x_2)<1<f(x_2), deci există a_1 între x_1 şi x_2 în care f(a_1)=1/f(x_2).
Pentru a_2=x_2: f(a_1)*f(a_2)=(1/f(x_2))*f(x_2)=1.