Fie (an)n>=1 , (bn)n>=1 definita astfel:
a1=4
a(n+1)=(2a4+27)/(3a4+2)
bn=(an-3)/(an+3) ; n>=1
a) Aratati ca (bn)n>=1 este progresie geometrica
b) Determinati an si bn.
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Fie (an)n>=1 , (bn)n>=1 definita astfel:
a1=4
a(n+1)=(2a4+27)/(3a4+2)
bn=(an-3)/(an+3) ; n>=1
a) Aratati ca (bn)n>=1 este progresie geometrica
b) Determinati an si bn.
Cred că ai vrut să scrii că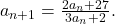
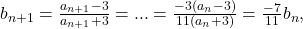
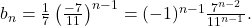
ceeace demonstrează că şirul (b_n) este o progresie geometrică cu raţia -7/11; cum b_1=1/7 obţii
Apoi, din relaţia de definiţie a lui b_n, scoţi a_n în funcţie de b_n şi finalizezi.