Buna ziua , o problema care nu imi da pace suna asa :
Fie o Matrice X patratica de 2 linii si 2 coloane cu proprietatea ca
matricea X^3 are pe prima linie ( 4 3) si pe a 2-a linie (-3 -2) => X = ?
Am reusit sa demonstrez ca daca in matricea X am nota elementele ei cu a,b,c,d , unde a,b sunt pe prima linie si b,c pe linia a 2a .. am demonstrat ca c=-b si ca a-d=2b . Si de aici m-am blocat ..


O finalizare posibilă.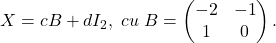 Acum
Acum
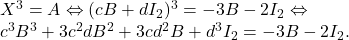
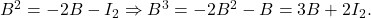
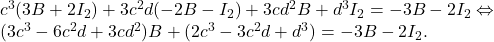
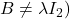 deducem sistemul:
deducem sistemul:
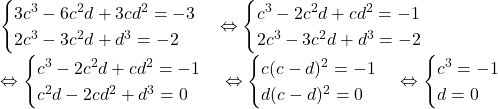
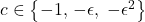
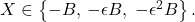
Scoţi b=-c, a=-2c+d şi deduci
Dar
Cu acestea ecuaţia se scrie
Pentru că matricele B şi I_2 sunt liniar independente (adică
deci d=0,