Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Bună seara!Mă puteti ajuta cu un exercitiu pentru admiterea la Universitatea Bucuresti, Facultatea de matematica si informatica?
Dacă intr-o progresie aritmetica exista un număr pătrar perfect,sa se demonstreze ca exista o infinitate.Am văzut ca intr-adevăr asa este si cred ca ar trebui sa fac inductie, ca sa demonstrez,dar nu stiu cum,precum si cum sa încep rezolvarea.
Va multumesc mult pentru timpul acordat.
Să zicem că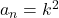
iar raţia progresiei este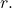 
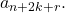
Calculaţi
L.E. Se subînţelege că progresia e formată din numere naturale, altfel proprietatea nu e adevărată.
Multumesc
Sau, fără inductie, din faptul că progresia contine un pătrat perfect rezultă că primul termen este rest pătratic modulo ratie de unde rezultă că există b astfel încât b^2 este congruent cu a(1) modulo r si ca urmare pătratul oricărui număr mai mare ca b^2 si congruent cu b modulo r este congruent cu a(1) modulo r deci apartine progresiei