Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
„Se consideră triunghiul ABC şi mijloacele M,N,P ale laturilor [AB ],[ BC],[CA ] . Fie I1, I2 şi I3 O1, O2 si O3 centrele cercurilor înscrise, respectiv circumscrise triunghiurilor , APN, BMP şi CNP (în această ordine). Arătaţi că triunghiurile I1I2I3 si O1O2O3 sunt congruente. ”
Asa suna problema. E la capitolul transformari geometrice in plan. Am facut figura de zece ori si nu reusesc sa identific centrul de rotatie, unghiul nici atat. (Presupunand ca nu gresesc si e vorba de rotatie.)
Asimetria din enunţ e suspectă. Verificaţi enunţul problemei.
Am verificat. Am incercat sa iau ca ultim triunghi CNA, ca sa aiba o „logica” alegerea triunghiurilor. Ar fi fost „varf, mijloc din stanga, mijloc latura opusa.Mai „inegale” triunghiurile.Am facut 10 figuri. Degeaba. Daca si dvs.ziceti ca e ceva incorect o las balta.
Cred că M e pe BC, N pe CA, P pe AB, iar triunghiurile sunt APN, BMP şi CNM.
În cazul ăsta, soluţia e omotetia. Indicaţie:
Am mers pe translatie. (Oricum era prima problema din tema, si prima transformare era translatia. Dar pe figura cu datele lor nu mergea NIMIC).
Am zis ca triunghiurile (dvs) sunt egale avand laturile egale si translatate cu un vector egal cu 1/2 din IO. Am demonstrat ca I1O1 =1/2 IO. Din asemanarea triunghiurilor:
-API1 si ABI2
-A01N SI AO2C
rezulta AI1O1 ~ AI2P2 cu k=1/2
deci I1O1=1/2 IO; similar se poate d3emonstra pentru I2O2 si I3O3
sper ca e bine
Faptul că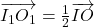
rezultă din omotetia care duce triunghiul ABC în triunghiul APN.
Aveti dreptate. Am luat-o „muncitoreste”. Cu ce imi era mai familiar. Asa demonstratia se simplifica si devine si foarte frumoasa. Multumesc.