Cum putem demonstra ca aceasta functie este injectiva?
greseala mea ,va rog sa ma scuzati,am modificat domeniul
![]()
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Conform definitiei, o functie ;f;A->B este injectiva daca pentru oricare doua elemente apartinand lui A-(a1 diferit de a2) exista f(a1) si f(a2), apartinand lui B si sunt diferite intre ele.
Asacum este data problema , nu se poate spune nimic pentru ca nu se prcizeaza domniul si codomeniul functiei. Daca f; R->R atunci FUNCTIA DATA ESTE injectiva.
Pentru x1 diferit de x2 in R, exista f(x1) , f(x2) in R si sunt diferite intre ele
Fie x1<x2 atunci f(x1)<fx2) ,in cazul dat , f(x) fiind continua si strict crescatoare este injectiva
De fapt toate functiile continui si strict crescatoare sau strict descrescatoare pot fi injective
O remarca donmnule DD, daca imi permiteti.
Orice functie strict cresctoare sau strict descrescatoare este injectiva, indiferent daca este continua sau nu.
@theangelov, uite o functie strict crescatoare, care nu este continua f(x)=x+[x].
Domnule ”Cristian”eu ma gandeam la functiile de tipul;(ex. f: R->R,unde;
……|=x penrtru x<,=4
f(x)=
……|=x-2 pentru x>4)
Buna ziua
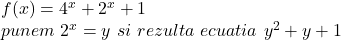
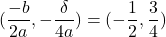
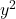 este pozitiv curba respectiva este convexa si ne gasim pe ramura ascendenta a curbei deci este cazul unei functii strict crescatoare deci injectiva.
este pozitiv curba respectiva este convexa si ne gasim pe ramura ascendenta a curbei deci este cazul unei functii strict crescatoare deci injectiva.
care este o paraola cu varful de cooordonate
Cum varful acestei parabole cade in stanga domeniului de definitie iar deoarece coeficientul lui