Sa se arate ca f este bijectiva si sa se calculeze fof:
f:N->N; f(n)=n+(-1)^n
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Sa se arate ca f este bijectiva si sa se calculeze fof:
f:N->N; f(n)=n+(-1)^n
Să verificăm dacă f este corect definită. f(n) este un număr natural ”vecin” cu n, cu excepţia, poate, a lui f(0); dar f(0)=0+(-1)^0=1.
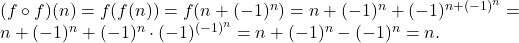
Acest vecin al lui 0 este număr natural, spre deosebire de -1. Deci funcţia este corect definită.
O caracterizare a funcţiilor bijective este:
f:A->B este bijectivă <=> pentru orice y din B, ecuaţia f(x)=y are o singură soluţie în A.
Fie m, arbitrar în N. f(n)=m <=> n+(-1)^n=m .
Dacă m este par, ”vecinul” său n este impar, deci ecuaţia este de fapt n-1=m cu soluţia unică n=m+1, număr natural.
Dacă m este impar, n trebuie să fie par: n+1=m are soluţia unică n=m-1, de asemenea număr natural.
In concluzie f este bijectivă.
adică inversa lui f este tot f.