1)Fie ABCD un patrulater convex ,E mijlocul segmentului (AB)si M apartine (BC), N apartine (AD) astfel incat BM/BC=AN/AD=k.
a)Sa se exprime vectorii EM si EN in functie de k si vectorii EA,EC,ED.
b)Sa se arate ca mijloacele segmentelor (AB),(MN) si (CD) sunt puncte coliniare.
2)Se considera ABCDEF un hexagon regulat si punctele M aprtine (AC) , N apartine (CE) astfel incat AM/AC=CN/CE=alfa .
a) Sa se exprime vectorii BM si BE in functie de alfa , AB si BC .
b)Sa se afle alfa stiind ca punctele B,M,N sunt coliniare .


Faceti un desen conf. problemei.
Se vede ca EAvector+ADvector=ED vector Cum ANvector=kADvactor=k(EDvector-EAvector) si la fel ;EBvector+BCvector=ECvector Cum BMvector=k.BCvector=k(ECvector-
-EBvector )=k(ECvector+EA vector). Deci;EMvector=EBvector+BMvctor=k.ECvector+(k-1)EAvector
(EAvector=-EBvector)
si ENvector=EAvector+ANvector=kEDvector+(1-k)EAvector
Fie P mijlocul lui MN si Q mijlocul lui CD
EM+EN=2EP=k(ED+EC)=k2EQ Cum vectorii EPsi EQ sunt colinari punctele ;E , P Q sunt colineare
Sa traiti ca ne-ati ajutat!
2). Relaţiile din ipoteză se scriu vectorial astfel: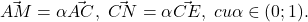
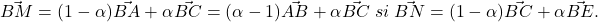
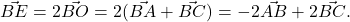
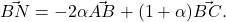
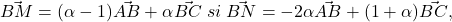
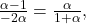 de unde se scoate valoarea convenabilă pentru alpha.
de unde se scoate valoarea convenabilă pentru alpha.
Conform echivalenţei dintre P2 si P3 de aici http://forum.matematic.ro/viewtopic.php?t=33516
avem şi
Într-un hexagon regulat co centrul O avem
Înlocuind se obţine
Punctele B, M, N sunt coliniare numai dacă sunt coliniari vectorii
lucru care se întâmplă numai dacă