Home/ Intrebari/Q 90661
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

elev98
Pe: 2015-11-14T12:44:23+02:00 In: In:

Limita

Calculati limitele sirurilor:
a) An=a^n / n! a>0
b) An=(2^n+3^n)/(3^n+4^n)

Multumesc anticipat!

Similare

8 raspunsuri

  1. DD
    profesor

    1)Fie k in N asa ca a^k/k!>=1Deci ; An=a^n/n! , n>k.-> 0<=An<1si pentru
    n->infinit An->0
    2)[3^n.((2/3)^n+1)]/[4^n((3/4)^n+1] sau (3/4)^n.((2/3^n+1)/((3/4)^n+1)
    pentru n->infinit limita xpresiei va fi ;0.(0+1)/(0+1)=0

  2. gefest

    La primul exercitiu limita este 0 pentru orice a real. Rezolvarea lui am gasit-o http://gen.lib.rus.ec/book/index.php?md5=3DC14B2AC498614596A6B473BC33D2EB la pagina 89 (se foloseste teorema lui Weierstrass).

  4. gigelmarga
    profesor

    gefest wrote: La primul exercitiu limita este 0 pentru orice a real. Rezolvarea lui am gasit-o http://gen.lib.rus.ec/book/index.php?md5=3DC14B2AC498614596A6B473BC33D2EB la pagina 89 (se foloseste teorema lui Weierstrass).

    Nu e nevoie de surse bibliografice sofisticate. Problema se găseşte cam în toate manualele.

    Abordarea optimă este criteriul raportului: fie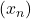 (x_n) un şir de numere strict pozitive astfel încât există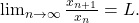 \lim_{n\to \infty}\frac{x_{n+1}}{x_n}=L.

    Atunci,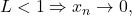 L<1 \Rightarrow x_n\rightarrow 0, iar L>1\Rightarrow x_n\rightarrow \infty.

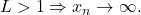
    În cazul nostru,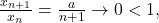 \frac{x_{n+1}}{x_n}=\frac{a}{n+1}\rightarrow 0<1, deci limita şirului este 0.

  5. gefest

    N-am prea rasfoit manualele de a 11-a, dar daca in acele manuale nu se demonstreaza asa-zisul criteriu al raportului, atunci si pe ele le-as numi pretentioase.

  6. gigelmarga
    profesor

    Manualul de la EDP

  8. gefest

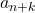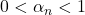    Dupa „Astfel a_{n+k}” cred ca era suficient <. In manualul de facultate de care am vorbit nu este mentionat acest criteriu, dar exemplul rezolvat acolo, cred, sugereaza ca este posibila si o alta demonstrare: din x_{n+1}<x_n rezulta ca exista un 0<\alpha_n<1 astfel incit 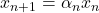x_{n+1}=\alpha_n x_n. Atunci limita 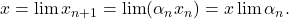x=\lim x_{n+1}=\lim(\alpha_n x_n)=x\lim\alpha_n. Dar mai este de aratat ca \lim\alpha_n\not=1.

  9. gigelmarga
    profesor

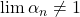    Există o demonstraţie mai „naturală”.

    Dacă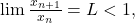 \lim\frac{x_{n+1}}{x_n}=L<1, atunci, de la un rang, avem 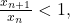\frac{x_{n+1}}{x_n}<1, deci şirul e descrescător. Cum e şi mărginit inferior, e convergent.

    Fie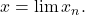 x=\lim x_n. Trecând la limită în egalitatea 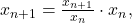x_{n+1}=\frac{x_{n+1}}{x_n}\cdot x_n, obţinem 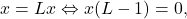x=Lx \Leftrightarrow x(L-1)=0, de unde x=0, căci L<1.

  10. gefest

    Da, n-am fost atent: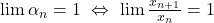 \lim\alpha_n=1\ \Leftrightarrow\ \lim\frac{x_{n+1}}{x_n}=1.

Raspunde

Raspunde