Home/ Intrebari/Q 90238
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

iwannalearnmath
Pe: 2015-09-05T12:11:54+03:00 In: In:

Functii de gradul 1.

1. Se considera functiile f,g:R->R , f(x)=1-x , g(x)=2x-1 . Demonstrati ca functia f compus g este strict descrescatoare
2. Se considera functia f:R->R , f(x)=ax+b . Sa se determine numerele reale a , b stiind ca 3f(x)+2=3x+8 .
3. Determinati functiile f:R->R de gradul 1 , pentru care f compus f =4x+3
Daca ma puteti ajuta 🙂
Multumesc !

Similare

2 raspunsuri

  1. adrianS

    Buna seara
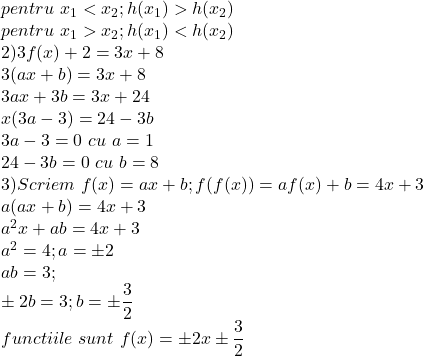
    1)Scriem:
    f(x)=1-x ; g(x)=2x-1
    f*g=f(g(x))=1-g(x)=1-2x+1=2-2x=h(x)
    h(x)este strict descrescatoare pentru ca
    pentru\ x_1<x_2 ; h(x_1)>h(x_2)\\ pentru \ x_1>x_2;h(x_1)<h(x_2)\\ 2)3f(x)+2=3x+8\\ 3(ax+b)=3x+8\\ 3ax+3b=3x+24\\ x(3a-3)=24-3b\\ 3a-3=0\ cu\ a=1\\ 24-3b=0\ cu\ b=8\\ 3)Scriem\ f(x)=ax+b;f(f(x))=af(x)+b=4x+3\\ a(ax+b)=4x+3\\ a^2x+ab=4x+3\\ a^2=4;a=\pm{2}\\ ab=3;\\ \pm{2b}=3;b=\pm{\dfrac{3}{2}}\\ functiile\ sunt\ f(x)=\pm{2}x\pm{\dfrac{3}{2}

  2. edy8
    maestru (V)

    adrianS wrote:
    3f(x)+2=3x+8

    3(ax+b)=3x+8

    adrianS wrote:
    f(x)=ax+b; f(f(x))=af(x)+b=4x+3

    a(ax+b)=4x+3

Raspunde

Raspunde