Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Buna ziua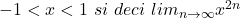 tinde la zero x fiind subnitar.
tinde la zero x fiind subnitar.
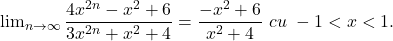
Parerea mea este ca pentru calculul limitei avem in vedere ca
Deci:
Multumesc frumos domule adrianS.Eu m-am complicat,am dat factor comun fortat pe cel mai mare.Cand defapt totul este atat de simplu!O seara placuta si toate cele bune!!:)
Cu placere
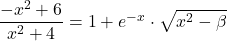 cu x=1 rezulta
cu x=1 rezulta
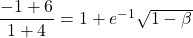 sau
sau
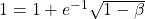 rezulta
rezulta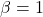
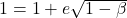 rezulta la fel
rezulta la fel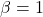
Sa continuam:
pentru ca functia sa fie continua trebuie ca limitele laterale fata de unu si fata de minus unu sa fie egale intre ele.
Atat pentru x=1 si x=-1 functia se comporta la fel din punct de vedere al limitelor laterale.
Astfel :
-pentru x=1 trebuie sa avem :
Analog pentru x=-1:
Deci raspunsul este punctul e.
Multumes pentru efortul depus.Va doresc multa sanatate si numai bine!Doamne ajuta!!!