z=1/4(radical din 3+i)
z^2014=?
Am scris pe z ca si z=[(radical 3)/4+1/4i]^2.Asta egal cu 1/4.Pe 1/4 l am ridicat la puterea 1007 ca sa ajung la puterea ceruta si rezultatu e 1/(2^2014).Raspunsul in carte e altul.Puteti sa-mi dati vreo idee.Multumesc!


Buna ziua
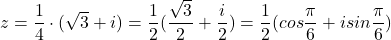
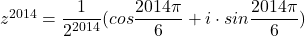
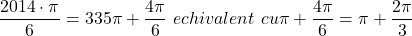
Scriem asa:
Ridicat la puterea 2014 rezulta dupa Moivre:
In continuare scriem ca
Functiile trigonometrice sunt pentru acest argument.
Multumesc mult!Dar nu am inteles de ce varianta mea nu a fost buna deoarece a fost printre variantele de raspuns si pare foarte logica..nu credeam ca trebuie aplicata Moivre.
Cum ai obtinut z=[(radical 3)/4+1/4i]^2 ?
Pai efectiv am inmultit 1/4 cu ce e in paranteza:)
Atunci trebuia sa obtii z=[(radical 3)/4+(1/4)i] si nu z=[(radical 3)/4+(1/4)i]^2
Oricum, iti recomand solutia lui adrianS.
Pai da… aia am obtinut in prima faza da dupa aceea am ridicat la a doua ca sa obtin ceva frumos..si mi-a mai ramas de ridicat la 1007 rezultatul obtinut adica 1/4.. dupa ce am ridicad la patrat