Sa se determine multimea valorilor parametrului real m pentru care sistemul este compatibil.

Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Buna ziua


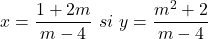 Introducem in ecuatia a treia a sistemului si gasim ca:
Introducem in ecuatia a treia a sistemului si gasim ca:
 de unde
de unde
 cu solutiile
cu solutiile 
 O alta varianta de rezolvare ar fi sa asiguram ca rangul matricii A a sistemului si rangul matricii extinse
O alta varianta de rezolvare ar fi sa asiguram ca rangul matricii A a sistemului si rangul matricii extinse  sa fie acelasi.
sa fie acelasi.
 si matricea extinsa si anume
si matricea extinsa si anume  pot avea un raqng comun de doi deoarece matricea A este de tip 3×2.Aceasta inseamna ca
pot avea un raqng comun de doi deoarece matricea A este de tip 3×2.Aceasta inseamna ca
 de unde rezulta ecuatia:
de unde rezulta ecuatia:
Sunt cred mai multe variante de rezolvare.
Una din ele ar fi:
retinem sistemul format din primele doua ecuatii si anume:
Rezolvam acest sistem dupa Cramer:
Pentru m=1 rezulta solutiile x=y=-1.
Aceste valori verifica si ecuatia trei din sistem.
Adica -1-1+2=0.Analog se procedeaza si cu celelalte doua valori pentru m.
Matricea sistemului si anume:
cu aceleasi solutii ca mai sus.