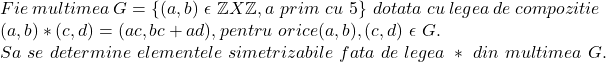
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Sa observam ca legea e comutativa. Determinam elementul neutru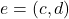 din relatia
din relatia 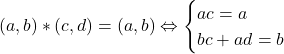 . Cum
. Cum 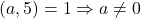 , deci din prima relatie obtinem
, deci din prima relatie obtinem 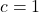 , iar din a doua, apoi,
, iar din a doua, apoi, 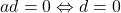 . Deci elementul neutru este
. Deci elementul neutru este 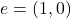 .
.
Daca e un element inversabil din
e un element inversabil din  in raport cu legea data, atunci exista un element
in raport cu legea data, atunci exista un element 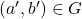 astfel incat
astfel incat 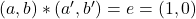 , echivalent cu sistemul
, echivalent cu sistemul 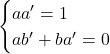 . Cum
. Cum 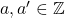 , rezulta
, rezulta 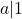 , deci
, deci 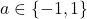 (Sa observam ca ambele valori verifica cerinta
(Sa observam ca ambele valori verifica cerinta 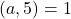 ). Daca
). Daca 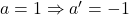 (care verifica
(care verifica 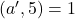 ), iar a doua relatie din sistem devine
), iar a doua relatie din sistem devine 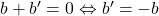 , adica toate elementele de forma
, adica toate elementele de forma 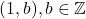 sunt inversabile, iar
sunt inversabile, iar 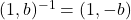 . Daca
. Daca  , avem
, avem 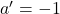 (care verifica
(care verifica 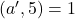 ), iar din a doua relatie deducem
), iar din a doua relatie deducem 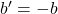 , adica toate elementele
, adica toate elementele 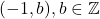 sunt inversabile si
sunt inversabile si 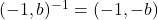 .
.
In concluzie, elementele inversabile din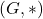 sunt cele de forma
sunt cele de forma 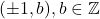 .
.
NOTA: Din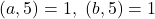 rezulta ca si
rezulta ca si 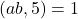 , deci legea e corect definita.
, deci legea e corect definita.
NOTA: Daca schimbam conditia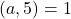 din definitia grupului cu
din definitia grupului cu  , obtinem aceleasi elemente inversabile.
, obtinem aceleasi elemente inversabile.
Multumesc !🙂