http://www.mathem.pub.ro/_SITE_ELEVI/p-set2.pdf
problema 14
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Imi place la nebunie modul in care abordati de fiecare data problemele.
http://www.mathem.pub.ro/_SITE_ELEVI/
Problema 64 mi se pare foarte interesanta… setul 7
Daca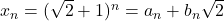
, atunci daca notam 
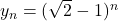, vom avea 
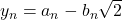(existenta numerelor 
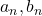, precum si relatia anterioara pentru 
se pot arata cu Binomul lui Newton).
Obtinem (adunand, respectiv scazand expresiile pentru
) 
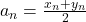, respectiv, 
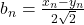, de unde limita ceruta este 
.
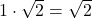Nu am inteles finalizarea si nu stiu nici sa demonstrez partea cu existenta..
An/Bn={[(1+sqrt(2))^n + (1-sqrt(2))^n ]/[ (1+sqrt(2))^n – (1-sqrt(2))^n]}*sqrt(2) , apoi imparti prin (1+sqrt(2))^n….cand treci la limita o sa ai un nr de forma [(1+a^n)/(1-a^n)]*sqrt(2) ,unde a este subunitar,deci limita lui a^n este 0….deci obtii 1*sqrt(2)…..scz ca am scris asa.