Calculati suma
1/3^2+2/15^2+3/35^2+4/63^2+…+ 50/9999^2
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Buna seara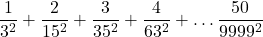
 Observam urmatoarea succesiune:numitorul este fomat dintr-un produs de patratul a doua numere care difera cu doi intre ele de ex.
Observam urmatoarea succesiune:numitorul este fomat dintr-un produs de patratul a doua numere care difera cu doi intre ele de ex.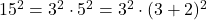 Aceasta ne facem sa scriem ultimul termen astfel:n(n+2)=9999.sau
Aceasta ne facem sa scriem ultimul termen astfel:n(n+2)=9999.sau
 o ecuatie de gradul doi cu solutia valabila n=99.
o ecuatie de gradul doi cu solutia valabila n=99. Grupele se rescriu astfel:
Grupele se rescriu astfel:
 Sirul devine deci:
Sirul devine deci:
 Se observa ca in suma se reduc succesiv termenii si ramane doar un singur termen egal cu
Se observa ca in suma se reduc succesiv termenii si ramane doar un singur termen egal cu 
Avem de calculat urmatoarea suma:
Suma o rescriem astfel:
Deci 9999=99×101.
Deci sirul va fi:
Intrebari?
Multumesc mult! Destul de complicat, nu m-as fi gandit!