1. (a/b-2)^2+(b/a+2)^2>=6, oricare ar fi a numar real fara o.
2. Aratati ca fractia 1x2x3x….x(n+1)/1x2x3x….x(n+1)+1 este ireductibila pentru orice n, numar natural fara 0.
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
1. (a/b-2)^2+(b/a+2)^2>=6, oricare ar fi a numar real fara o.
2. Aratati ca fractia 1x2x3x….x(n+1)/1x2x3x….x(n+1)+1 este ireductibila pentru orice n, numar natural fara 0.
Salut,
Exerciţiul 2 se rezolvă prin reducere la absurd.
Notăm cu p = 1 x 2 x 3 x … n x (n+1), fracţia devine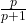
.
Presupunem că fracţia e reductibilă, adică există d care divide atât pe numitor, cât şi pe numărător:
d | p+1
d | p.
Dacă există un asemenea divizor, atunci d | p+1-p = 1, adică d | 1. Asta înseamnă că p şi p+1 sunt prime între ele, ceea ce contrazice ipoteza de la începutul rezolvării.
Ipoteza este deci falsă, adică fracţia este ireductibilă.
Green eyes.