![]()
Sursa:Culegerea de politehnică,editura U.T.PRESS
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
o radacina ,intre 0 si 1
Functia este crescatoare pe (0,inf).
Pentru rezultat final, mai folosesti si postul lui nica10, eventual.
Derivata polinomului va fi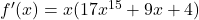 . Sa notam cu
. Sa notam cu  functia din paranteza. Datorita faptului ca limitele acestei functii la minus si plus infinit sunt, respectiv, minus infinit si plus infinit si a faptului ca functia e continua, rezulta ca ea are cel putin o radacina reala. Deoarece
functia din paranteza. Datorita faptului ca limitele acestei functii la minus si plus infinit sunt, respectiv, minus infinit si plus infinit si a faptului ca functia e continua, rezulta ca ea are cel putin o radacina reala. Deoarece 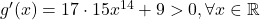 , rezulta ca functia e strict crescatoare, deci injectiva. In concluzie,
, rezulta ca functia e strict crescatoare, deci injectiva. In concluzie,  are o singura radacina reala. Ne intereseaza pozitia acesteia fata de zero. Avem
are o singura radacina reala. Ne intereseaza pozitia acesteia fata de zero. Avem 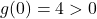 , deci radacina e in
, deci radacina e in  . Atunci singura radacina pozitiva a lui
. Atunci singura radacina pozitiva a lui 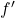 este
este  . Cum
. Cum 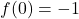 , iar cum limita polinomului la plus infinit este infinit, din sirul lui Rolle, ecuatia din enunt are o singura radacina pozitiva.
, iar cum limita polinomului la plus infinit este infinit, din sirul lui Rolle, ecuatia din enunt are o singura radacina pozitiva.
EDIT: Frumoasa ideea domnului A_Cristian🙂 .. intr-adevar, pe  functia este suma de functii strict crescatoare (si o functie constanta), deci strict crescatoare. Urmeaza ca e injectiva, deci are cel mult o radacina. Pentru demonstratia ca exista o radacina, putem considera si
functia este suma de functii strict crescatoare (si o functie constanta), deci strict crescatoare. Urmeaza ca e injectiva, deci are cel mult o radacina. Pentru demonstratia ca exista o radacina, putem considera si 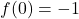 si limita la plus infinit sau, alternativa pentru limita, dupa cum e sugerat si de posturile domnilor A_Cristian si nica10, se poate lua
si limita la plus infinit sau, alternativa pentru limita, dupa cum e sugerat si de posturile domnilor A_Cristian si nica10, se poate lua 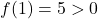 .
.