Să se calculeze 
stiind că 
.
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Care este domeniul lui f?
Nu cred că este necesar de stabilit domeniul de definitie al functiei f(x) deoarece mai întâi această functie f(x) trebuie găsită.
Atunci pentru care x este adevarata relatia de mai sus? Sau si asta trebuie dedus din relatie?
Ori cineva mi-a modificat enunţul problemei ori eu am greşit!!??
Dăcă am greşit eu,atunci rectific enunţul problemei (am reeditat şi prima postare):
Să se calculeze
x^2+2x+3 ,eu cred ca ideea este sa punem un x in expresia lui f(x^2…) astfel incat punand acel x sa obtinem chiar x .
Enuntul a fost acelasi. Cel putin eu nu sesizez vreo diferenta.
Eu am intrebat insa altceva. Pentru care x este valabila aceasta relatie? Este valabila pentru tot domeniul de definitia al lui f? Pentru niste puncte bine stabilite?
De exemplu, pot spune ca f(x)=x+7 pt orice x real, iar relatia este adevarat doar pentru un numar limtat de valori.
In cazul care incepem sa speculam si sa obtine niste intervale cat mai mari, relatia poate fi definita corect fie pe (-inf,-1/3] fie pe [-1/3,inf).
Daca eu imi aleg convenabil sa tratez cazul cand relatia de mai sus este adevarata pentru orice x>=1, atunci problema capata o alta turnura.
O tentativa de abordare este urmatoarea:
N-am mai inclus si calculul final si nici nu am de gand sa fac asta.
Atata timp cat nu precizati conditiile problemei si lasati cea mai mare parte in seama speculei, va puteti astepta la orice raspuns.
PS: Alegerea lui x>=1 nu este pur intamplatoare.
Noi avem date concrete despre f doar pe un eventual interval [2,inf). Astfel, 3x^2+2x+1>=2 si cum am consideram ca iau intervalul pentru care x este si pozitiv, atunci x>=1. Atlfe ajungem iar pe taramul speculatiilor.
Nu am înţeles raţionamentul Dvs..
Raţionamentul meu este mai simplu:
Rezolvare în trei paşi:
1) Înlocuim
cu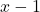 
şi deci 
.
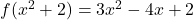2) Înlocuim
cu 
şi deci 
.
3) Înlocuim
cu 
şi deci 
.
Domeniul de definiţie si de valori se stabileşte foarte uşor pentru funcţia
.
Eu consider ca ar fi bine sa mergem cu solutia pana la capat.
Pentru ce x are loc relatia data?
Pentru x=0, cat este f(3x^2+2x+1)?!
De aici a pornit discutia mea si solutia mea. In rest functiile sunt aproape identice, domeniul de definitie nefiind precizat in cazul dumneavoastra, dar banuiesc ca ar fi [2,inf).
Problema cere care este
–––––––––––
De analiza complexa şi deci despre teoria funcţiilor de variabilă complexă aţi auzit?
Consider ca nu are sens sa va mai bag in seama.
Acest site este pentru elevi de liceu.
Programa pentru liceu nu cuprinde functii de variabila complexa decat tangential (in special functii polinomiale). Aratati-mi in manual sau programa tratarea functiei radical pe numere complexe.
Iar peste numere complexe este o prostie ce incercati sa definiti functia dumneavoastra. Macar puteti s-o definiti peste R asa cum vreti dumneavoastra?
Cat este f(0)? Dar f(3)? Asta conform relatiei pe care ati vrut s-o dati.
Repet:
Ce înseamnă după părerea Dvs. secţiunea „Alte probleme
Probleme deschise, greu sau
Dvs. aţi intrat la această secţiune fără să citţi la ce anume se referă…Deci înainte de a jigni pe cineva v-aş ruga să postaţi la celelate secţiuni şi anume cele de la clasele III-XII….Nu v-am rugat eu să vă băgaţi pe această secţiune şi nici nu vreau să fiu băgat în seamă….dar aş dori părerea altor forumişti mai buni decât noi…Mulţumesc pentru colaborare!Numai bine!